题目内容
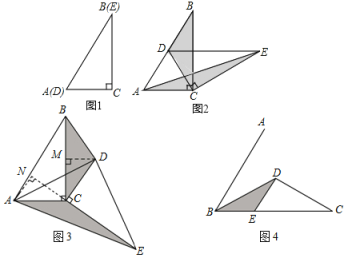
【题目】在△ABC中,AD为BC边上的中线,E为AD上一动点,设DE=nEA,连接CE并延长,交AB于点F.
(1)尝试探究:如图1,当∠BAC=90°,∠B=30°,DE=EA时,BF,BA之间的数量关系是 ;
(2)类比延伸:如图2,当△ABC为锐角三角形,DE=EA时,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;
(3)拓展迁移:如图3,当△ABC为锐角三角形,DE=nEA时,请直接写出BF,BA之间的数量关系.
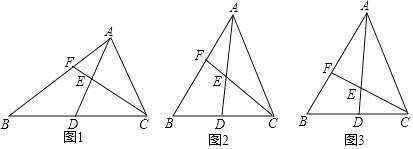
【答案】(1)![]() ;(2)仍然成立,见解析;(3)
;(2)仍然成立,见解析;(3)![]()
【解析】
(1)尝试探究:过点![]() 作
作![]() ,交
,交![]() 于
于![]() ,可证
,可证![]() ,
,
,![]() ,可得
,可得![]() ,可证
,可证![]() ,
,
可得BF,BA之间的数量关系;
(2)类比延伸:过点![]() 作
作![]() ,交
,交![]() 于
于![]() ,可证
,可证![]() ,
,![]() ,可得
,可得![]() ,可证
,可证![]() ,可得
,可得![]() 之间的数量关系;
之间的数量关系;
(3)拓展迁移:过点![]() 作
作![]() ,交
,交![]() 于
于![]() ,由平行线分线段成比例可得
,由平行线分线段成比例可得![]() ,可得
,可得![]() ,即可求
,即可求![]() 之间的数量关系.
之间的数量关系.
解:(1)尝试探究
如图,过点![]() 作
作![]() ,交
,交![]() 于
于![]()

∵![]() 是中线,
是中线,![]()
∴![]()
∵![]() ,
,
∴![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
(2)类比延伸:
结论仍然成立,
理由如下:
如图,过点![]() 作
作![]() ,交
,交![]() 于
于![]()

∵![]() 是中线,
是中线,![]()
∴![]()
∵![]() ,
,
∴![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
(3)拓展迁移
如图,过点![]() 作
作![]() ,交
,交![]() 于
于![]()

∵![]() ,且
,且![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
![]()
∴![]()

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目