题目内容
已知点P（x，y）满足等式x2+y2-4x+6y+13=0，则点P关于原点对称的点的坐标为（ ）
| A、（-2，3） |
| B、（-2．-3） |
| C、（2，-3） |
| D、（2，3） |
考点：关于原点对称的点的坐标,非负数的性质：偶次方,配方法的应用
专题：
分析：本题比较容易，考查平面直角坐标系中任意一点P（x，y），关于原点的对称点是（-x，-y），等式x2+y2-4x+6y+13=0可化为（x-2）2+（y+3）2=0，可解得x与y的值，求点P关于原点的对称点的坐标就是把横纵坐标都变成相反数．
解答：解：∵等式x2+y2-4x+6y+13=0可化为（x-2）2+（y+3）2=0，
∴x-2=0，y+3=0，
x=2，y=-3，
∴P关于原点的对称点的坐标是（-2，3），
故选：A．
∴x-2=0，y+3=0，
x=2，y=-3，
∴P关于原点的对称点的坐标是（-2，3），
故选：A．
点评：关于原点对称的点坐标的关系，是需要识记的基本问题．并且本题又考查了任何数的平方值是非负数．
练习册系列答案
相关题目
如图，从A地到B地走二次根式
有意义x的取值范围是（ ）
| x+5 |
| A、x≥-5 | B、x≤5 |
| C、x≤-5 | D、x＜-5 |
用配方法解下列方程时，配方有误的是（ ）
| A、x2-2x-99=0化为（x-1）2=100 | ||||
B、2y2-7y-4=0化为（y-
| ||||
| C、x2-8x+4=0化为（x-2）2=0 | ||||
| D、x2+6x-5=0化为（x+3）2=14 |
已知二次函数y=kx2-7x-7的图象与x轴有两个交点，则k的取值范围为（ ）
A、k＞-
| ||
B、k＞-
| ||
C、k≥-
| ||
D、k≥-
|
如图，C为线段AB的中点，N为线段CB的中点，CN=1cm．求线段CB、线段AC、线段AB的长．
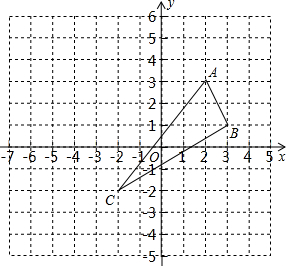如图，已知△ABC的三个顶点分别为A（2，3），B（3，1），C（-2，-2），