题目内容
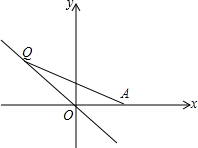 如图,点Q在直线y=-x上运动,点A的坐标为(4,0),当线段AQ最短时,点Q的坐标为
如图,点Q在直线y=-x上运动,点A的坐标为(4,0),当线段AQ最短时,点Q的坐标为考点:一次函数图象上点的坐标特征,垂线段最短
专题:计算题
分析:过A作AP⊥直线y=-x于P,作PB⊥x轴于B,如图,由于直线y=-x为第二、四象限的角平分线,则∠AOP=45°,于是可判断△PAO为等腰直角三角形,利用等腰直角三角形的性质得OB=AB=2,PB=
OA=
×4=2,则P点坐标为( )2,-2),然后根据垂线段最短得到点Q(2,-2)时,线段AQ最短.
| 1 |
| 2 |
| 1 |
| 2 |
解答: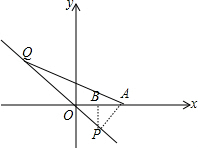 解:过A作AP⊥直线y=-x于P,作PB⊥x轴于B,如图,
解:过A作AP⊥直线y=-x于P,作PB⊥x轴于B,如图,
∵直线y=-x为第二、四象限的角平分线,
∴∠AOP=45°,
∴△PAO为等腰直角三角形,
∵PB⊥OA,
∴OB=AB=2,PB=
OA=
×4=2,
∴P点坐标为(2,-2),
∴当点Q运动到点P的位置时,线段AQ最短,此时Q点坐标为(2,-2).
故答案为(2,-2).
 解:过A作AP⊥直线y=-x于P,作PB⊥x轴于B,如图,
解:过A作AP⊥直线y=-x于P,作PB⊥x轴于B,如图,∵直线y=-x为第二、四象限的角平分线,
∴∠AOP=45°,
∴△PAO为等腰直角三角形,
∵PB⊥OA,
∴OB=AB=2,PB=
| 1 |
| 2 |
| 1 |
| 2 |
∴P点坐标为(2,-2),
∴当点Q运动到点P的位置时,线段AQ最短,此时Q点坐标为(2,-2).
故答案为(2,-2).
点评:本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-
,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.也考查了垂线段最短和等腰直角三角形的性质.
| b |
| k |

练习册系列答案
相关题目
已知在坐标平面内有一点M(3,4),点M关于原点的对称点为N,则点M和点N的距离( )
| A、6 | B、8 | C、10 | D、12 |
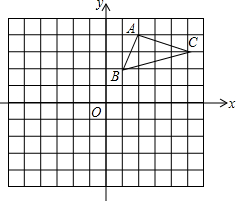 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题: