题目内容
5. 如图,△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,点F在AC上,BD=DF,求证:CF=BE.
如图,△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,点F在AC上,BD=DF,求证:CF=BE.
分析 根据角平分线的性质可以得出DC=DE,由HL证明△DCF≌△DEB,得出对应边相等即可.
解答 证明:∵∠C=90°,
∴DC⊥AC.
∵AD是∠BAC的平分线,DE⊥AB,
∴DC=DE.
在Rt△DCF和Rt△DEB中,$\left\{\begin{array}{l}{DF=BD}\\{DC=DE}\end{array}\right.$,
∴Rt△DCF≌Rt△DEB(HL),
∴CF=EB.
点评 本题考查了角平分线的性质的运用,全等三角形的判定与性质的运用;熟记角平分线的性质定理,证明三角形全等是解决问题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
15.十八世纪瑞士数学家欧拉证明了简单多面体的顶点数(V)、面树(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:
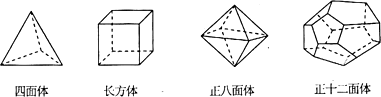
(1)根据上面多面体模型,填写表格中的空格:
(2)根据上面的表格,猜想顶点数(V)、面数(F)、棱数(E)之间存在的关系式是V+F-E=2(用所给的字母表达);
(2)若一个多面体的面数比顶点数少14,且有48条棱,则这个多面体的面数是18;
(3)有一个玻璃饰品的外形是简单多面体,它共有24个顶点,每个顶点处都有3条棱,设该多面体的面数为x,求x的值.

(1)根据上面多面体模型,填写表格中的空格:
| 多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
| 四面体 | 4 | 4 | 6 |
| 长方体 | 8 | 6 | 12 |
| 正八面体 | 6 | 8 | 12 |
| 正十二面体 | 20 | 12 | 30 |
(2)若一个多面体的面数比顶点数少14,且有48条棱,则这个多面体的面数是18;
(3)有一个玻璃饰品的外形是简单多面体,它共有24个顶点,每个顶点处都有3条棱,设该多面体的面数为x,求x的值.
13. 如图,△ABC是等边三角形,CB=BD,连接AD,∠ACD=110°,则∠BAD的度数为( )
如图,△ABC是等边三角形,CB=BD,连接AD,∠ACD=110°,则∠BAD的度数为( )
 如图,△ABC是等边三角形,CB=BD,连接AD,∠ACD=110°,则∠BAD的度数为( )
如图,△ABC是等边三角形,CB=BD,连接AD,∠ACD=110°,则∠BAD的度数为( )| A. | 10° | B. | 15° | C. | 20° | D. | 25° |
10.关于x的方程x2+2kx-1=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 无实数根 | D. | 不能确定 |
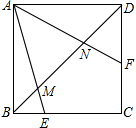 如图,正方形ABCD中,点E、F分别是BC、CD边上的点,且∠EAF=45°,对角线BD交AE于点M,交AF于点N.若AB=4$\sqrt{2}$,BM=2,则MN的长为$\frac{10}{3}$.
如图,正方形ABCD中,点E、F分别是BC、CD边上的点,且∠EAF=45°,对角线BD交AE于点M,交AF于点N.若AB=4$\sqrt{2}$,BM=2,则MN的长为$\frac{10}{3}$.