题目内容
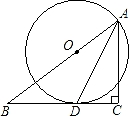
如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C,则点B转过的路径长为( )

A. B.
B. C.
C. D.π
D.π
B.
【考点】旋转的性质;弧长的计算.
【专题】几何图形问题.
【分析】利用锐角三角函数关系得出BC的长,进而利用旋转的性质得出∠BCB′=60°,再利用弧长公式求出即可.
【解答】解:∵在△ABC中,∠ACB=90°,∠ABC=30°,AB=2,
∴cos30°= ,
,
∴BC=ABcos30°=2×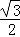 =
= ,
,
∵将△ABC绕直角顶点C逆时针旋转60°得△A′B′C,
∴∠BCB′=60°,
∴点B转过的路径长为: =
= π.
π.
故选:B.
【点评】此题主要考查了旋转的性质以及弧长公式应用,得出点B转过的路径形状是解题关键.

练习册系列答案
相关题目
 B.
B. C.
C. D.
D.

 +x2+1=0
+x2+1=0
 B.
B. 
 D.
D.