题目内容
如图，已知∠BDC=140°，∠B=34°，∠C=28°，则∠A=考点：三角形的外角性质,三角形内角和定理
专题：
分析：延长BD交AC于E，根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CED，再求出∠A即可．
解答：解：如图，延长BD交AC于E，
∵∠BDC=140°，∠C=28°，
∴∠CED=∠BDC-∠C=140°-28°=112°，
又∵∠B=34°，
∴∠A=∠CED-∠B=112°-34°=78°．
故答案为：78°．
∵∠BDC=140°，∠C=28°，
∴∠CED=∠BDC-∠C=140°-28°=112°，
又∵∠B=34°，
∴∠A=∠CED-∠B=112°-34°=78°．
故答案为：78°．
点评：本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质，作辅助线构造出两个三角形是解题的关键．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
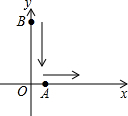如图，两条直线互相垂直于点O，点A位于O处，以2cm/s的速度向右匀速移动，点B位于O的正上方18cm处，以3cm/s的速度与A同时开始向下匀速移动，多长时间时△AOB的面积为24cm2？