题目内容
8．写出以3，-5为根且二次项系数为1的一元二次方程是x2+2x-15=0．分析 先计算出3与-5的和与积，然后根据根与系数的关系写出满足条件的一元二次方程．
解答 解：∵3+（-5）=-2，3×（-5）=-15，
∴以3，-5为根且二次项系数为1的一元二次方程是x2+2x-15=0，
故答案为x2+2x-15=0．
点评 本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．
练习册系列答案
阅读快车系列答案
相关题目
18．如图所示，用1个边长为c的小正方形和直角边长分别为a，b的4个直角三角形，恰好能拼成一个新的大正方形，其中a，b，c满足等式c2=a2+b2，由此可验证的乘法公式是（ ）
| A． | a2+2ab+b2=（a+b）2 | B． | a2-2ab+b2=（a-b）2 | C． | （a+b）（a-b）=a2-b2 | D． | a2+b2=（a+b）2 |
19．在平面直角坐标系中，点P（-1，1）位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
16．如果a＜b，下列各式中不一定正确的是（ ）
| A． | a-1＜b-1 | B． | $\frac{1}{a}$＜$\frac{1}{b}$ | C． | -3a＞-3b | D． | $\frac{a}{4}$＜$\frac{b}{4}$ |
3．下列各式中，与$\sqrt{2}$是同类二次根式的是（ ）
| A． | $\sqrt{3}$ | B． | $\sqrt{5}$ | C． | $\sqrt{8}$ | D． | $\sqrt{14}$ |
13．下列式子中，属于最简二次根式的是（ ）
| A． | $\sqrt{16}$ | B． | $\sqrt{6}$ | C． | $\sqrt{28}$ | D． | $\sqrt{\frac{1}{5}}$ |
17．过A（-5，-4）和B（-5，4）两点的直线一定（ ）
| A． | 垂直于x轴 | B． | 与x轴相交但不平行于x轴 | ||
| C． | 平行于x轴 | D． | 与x轴、y轴都不平行 |
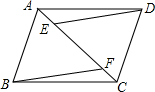如图，已知四边形ABCD中，连接AC，点E、F在AC上，AE=CF，连接DE，BF，且DE$\underset{∥}{=}$BF，求证：四边形ABCD是平行四边形．