题目内容
5.若等腰三角形的一边长为6,另两边长分别是关于x的方程x2-(m+2)x+2m+4=0的两个根,求m的值.分析 分底为6和腰为6两种情况考虑:底为6时,则方程有两个相等的实数根,利用根的判别式△=0即可求出m的值;腰为6时,将x=6代入原方程求出m的值.综上即可得出结论.
解答 解:当底为6时,另两边为腰,即方程x2-(m+2)x+2m+4=0有两个相等的实数根,
∴△=[-(m+2)]2-4×1×(2m+4)=0,
解得:m=6或m=-2,
当m=-2时,方程x2-(m+2)x+2m+4=0的两个根为0,不符合题意,
当m=6时,原方程为x2-8x+16=(x-4)2=0,
此时方程的两个根为4,
∵4,4,6能为三角形的三条边,
∴m=6成立;
当腰为6时,将x=6代入x2-(m+2)x+2m+4=0中,
得:36-6(m+2)+2(m+2)=0,
解得:m=7,
当m=7时,原方程为x2-9x+18=(x-3)(x-6)=0,
解得:x=3,或x=6,
∵3,6,6能为三角形的三条边,
∴m=7成立.
综上可知:m的值为6或7.
点评 本题考查了根的判别式、一元二次方程的解以及等腰三角形的性质,解题的关键是分底为6和腰为6两种情况考虑.本题属于基础题,难度不大,解决该题型题目时,根据等腰三角形边的性质分情况讨论是关键.

练习册系列答案
相关题目
3.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
13.星星果汁店中的A种果汁比B种果汁每杯贵1元,小彬和同学买了3杯B种果汁,2杯A种果汁,一共花了16元,A种果汁B种果汁每杯分别多少元?设A种果汁的单价为x元,B种果汁的单价为y元,则以下方程组正确的是( )
| A. | $\left\{\begin{array}{l}{3x+2y=16}\\{x=y+1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+3y=16}\\{x=y-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{2x+3y=16}\\{x=y+1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{3x+2y=16}\\{x=y-1}\end{array}\right.$ |
14.下列各组数中,不能构成直角三角形的是( )
| A. | $\sqrt{5}$,$\sqrt{12}$,$\sqrt{13}$ | B. | 1,$\sqrt{2}$,$\sqrt{3}$ | C. | 3,4,5 | D. | 6,8,10 |
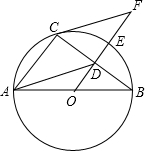 如图,AB为圆O的直径,点C、E在圆上,且点E是弧BC的中点,OE交弦BC于点D,点F在OE的延长线上,且∠BCF=∠BAC,BC=8,DE=2.
如图,AB为圆O的直径,点C、E在圆上,且点E是弧BC的中点,OE交弦BC于点D,点F在OE的延长线上,且∠BCF=∠BAC,BC=8,DE=2.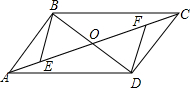 如图,?ABCD的对角线AC、BD相交于点O,OE=OF.
如图,?ABCD的对角线AC、BD相交于点O,OE=OF.