题目内容
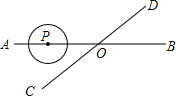 如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在直线AB上,开始时,PO=8cm,如果⊙P以2cm/秒的速度沿直线由A向B移动,那么当⊙P的运动时间t(秒)满足条件
如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在直线AB上,开始时,PO=8cm,如果⊙P以2cm/秒的速度沿直线由A向B移动,那么当⊙P的运动时间t(秒)满足条件考点:直线与圆的位置关系
专题:
分析:求得当⊙P位于点O的左边与CD相切时t的值和⊙P位于点O的右边与CD相切时t的值,两值之间即为相交.
解答:解:当点P在射线OA时⊙P与CD相切,如图,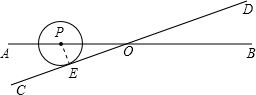 过P作PE⊥CD与E,
过P作PE⊥CD与E,
∴PE=1cm,
∵∠AOC=30°,
∴OP=2PE=2cm,
∴⊙P的圆心在直线AB上向右移动了(8-2)cm后与CD相切,
∴⊙P移动所用的时间=
=3(秒);
当点P在射线OB时⊙P与CD相切,如图,过P作PE⊥CD与F,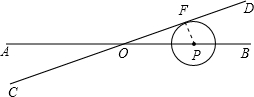
∴PF=1cm,
∵∠AOC=∠DOB=30°,
∴OP=2PF=2cm,
∴⊙P的圆心在直线AB上向右移动了(8+2)cm后与CD相切,
∴⊙P移动所用的时间=
=5(秒).
当⊙P的运动时间t(s)满足条件3<t<5时,⊙P与直线CD相交.
故答案为:3<t<5.
 过P作PE⊥CD与E,
过P作PE⊥CD与E,∴PE=1cm,
∵∠AOC=30°,
∴OP=2PE=2cm,
∴⊙P的圆心在直线AB上向右移动了(8-2)cm后与CD相切,
∴⊙P移动所用的时间=
| 8-2 |
| 2 |
当点P在射线OB时⊙P与CD相切,如图,过P作PE⊥CD与F,

∴PF=1cm,
∵∠AOC=∠DOB=30°,
∴OP=2PF=2cm,
∴⊙P的圆心在直线AB上向右移动了(8+2)cm后与CD相切,
∴⊙P移动所用的时间=
| 8+2 |
| 2 |
当⊙P的运动时间t(s)满足条件3<t<5时,⊙P与直线CD相交.
故答案为:3<t<5.
点评:本题考查了直线与圆的位置关系:直线与有三种位置关系(相切、相交、相离).也考查了切线的性质.

练习册系列答案
相关题目
已知一个班级40人,数学老师第一次统计这个班的平均成绩为85分,在复查时发现漏记了一个学生的成绩80分,那么这个班的实际平均成绩应为( )
| A、85分 | B、84.875分 |
| C、87分 | D、84.5分 |
如果
=2-2a,则( )
| (2a-2)2 |
| A、a<1 | B、a≤1 |
| C、a>1 | D、a≥1 |
 如图,利用一面墙,用80米长的篱笆围成一个矩形场地
如图,利用一面墙,用80米长的篱笆围成一个矩形场地