题目内容
 如图,利用一面墙,用80米长的篱笆围成一个矩形场地
如图,利用一面墙,用80米长的篱笆围成一个矩形场地(1)怎样围才能使矩形场地的面积为750平方米?
(2)能否使所围的矩形场地面积为810平方米,为什么?
考点:一元二次方程的应用
专题:几何图形问题
分析:(1)设和墙平行的篱笆的长度是x米,根据利用一面墙,用80m长的篱笆围一个矩形场地面积为750平方米,从而可列方程求解.
(2)假使矩形面积为810,则x无实数根,所以不能围成矩形场地.
(2)假使矩形面积为810,则x无实数根,所以不能围成矩形场地.
解答:解:(1)由题意得:x(80-2x)=720,
解得:x1=15 x2=25,
当x=15时,AD=BC=15m,AB=50m,
当x=25时,AD=BC=25m,AB=30m,
答:当平行于墙面的边长为50m,斜边长为15m时,矩形场地面积为750m2;
或当平行于墙面的边长为30m,邻边长为25m时矩形场地面积为750m2.
(2)由题意得:x(80-2x)=810,
△=40-4×405=1600-1620=-20<0,
∴方程无解,即不能围成面积为810m2的矩形场地.
解得:x1=15 x2=25,
当x=15时,AD=BC=15m,AB=50m,
当x=25时,AD=BC=25m,AB=30m,
答:当平行于墙面的边长为50m,斜边长为15m时,矩形场地面积为750m2;
或当平行于墙面的边长为30m,邻边长为25m时矩形场地面积为750m2.
(2)由题意得:x(80-2x)=810,
△=40-4×405=1600-1620=-20<0,
∴方程无解,即不能围成面积为810m2的矩形场地.
点评:此题不仅是一道实际问题,而且结合了矩形的性质,解答此题要注意以下问题:
(1)矩形的一边为墙,且墙的长度不超过45米;
(2)根据矩形的面积公式列一元二次方程并根据根的判别式来判断是否两边长相等.
(1)矩形的一边为墙,且墙的长度不超过45米;
(2)根据矩形的面积公式列一元二次方程并根据根的判别式来判断是否两边长相等.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
已知△ADE与△ABC的相似比为1:2,则△ADE与△ABC的周长比为( )
| A、1:2 | B、1:4 |
| C、2:1 | D、4:1 |
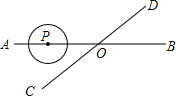 如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在直线AB上,开始时,PO=8cm,如果⊙P以2cm/秒的速度沿直线由A向B移动,那么当⊙P的运动时间t(秒)满足条件
如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在直线AB上,开始时,PO=8cm,如果⊙P以2cm/秒的速度沿直线由A向B移动,那么当⊙P的运动时间t(秒)满足条件