题目内容
有n个数,第一个记为a1,第二个记为a2,…,第n个记为an.若a1=
,且从第二个数起,每个数都等于“1与它前面那个数的差的倒数”.
(1)求a2,a3,a4的值;
(2)根据(1)的计算结果,请你猜想并写出a2014,a2015,a2016的值;
(3)计算:a1•a2•a3•…a2014•a2015•a2016.
| 1 |
| 2 |
(1)求a2,a3,a4的值;
(2)根据(1)的计算结果,请你猜想并写出a2014,a2015,a2016的值;
(3)计算:a1•a2•a3•…a2014•a2015•a2016.
考点:规律型:数字的变化类,倒数
专题:
分析:(1)根据a1=
和每个数都等于“1与它前面那个数的差的倒数”,分别列出算式,再进行计算即可;
(2)根据(1)得出的规律,每三个数循环一次,用2014、2015、2016分别除以3,即可得出答案;
(3)根据得出的规律每三个数循环一次,三个数相乘得(-1).再看(-1)的个数,即可得出答案.
| 1 |
| 2 |
(2)根据(1)得出的规律,每三个数循环一次,用2014、2015、2016分别除以3,即可得出答案;
(3)根据得出的规律每三个数循环一次,三个数相乘得(-1).再看(-1)的个数,即可得出答案.
解答:解:(1)∵a1=
,
∴a2=
=2,
a3=
=-1,
a4=
=
;
(2)根据(1)的计算可以得到a1=a4,则这些数三个数循环一次,
2014÷3=671…1,则a2014=a1=
;
2015÷3=671…2,则a2014=a2=2;
2016÷3=672,则a2014=a3=-1;
(3)根据题意得:
a1•a2•a3•…a2014•a2015•a2016=
×2×(-1)×…×
×2×(-1)=1.
| 1 |
| 2 |
∴a2=
| 1 | ||
1-
|
a3=
| 1 |
| 1-2 |
a4=
| 1 |
| 1-(-1) |
| 1 |
| 2 |
(2)根据(1)的计算可以得到a1=a4,则这些数三个数循环一次,
2014÷3=671…1,则a2014=a1=
| 1 |
| 2 |
2015÷3=671…2,则a2014=a2=2;
2016÷3=672,则a2014=a3=-1;
(3)根据题意得:
a1•a2•a3•…a2014•a2015•a2016=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了数字的变化类,用到的知识点是倒数、有理数的运算,正确理解结果的循环的规律是本题的关键.

练习册系列答案
相关题目
已知ax|a|-1+8=2(x-2)是关于x的一元一次方程,则( )
| A、a≠2 | B、a=±1或-2 |
| C、a=±1 | D、a=-2 |
若直线y=-3x+m与两坐标轴所围成的三角形的面积是6,则m的值为( )
| A、6 | B、-6 | C、±6 | D、±3 |
当m是正整数时,下列等式不一定成立的有( )
| A、a2m=(am)2 |
| B、a2m=(a2)m |
| C、a2m=(-am)2 |
| D、a2m=(-a2)m |
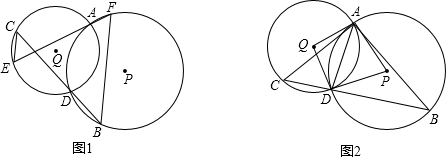
 如图,△ABC内的线段BD、CE相交于点O,已知OB=OD,OC=2OE,设△BOE、△BOC、△COD和四边形AEOD的面积,分别为S1、S2、S3和S4.
如图,△ABC内的线段BD、CE相交于点O,已知OB=OD,OC=2OE,设△BOE、△BOC、△COD和四边形AEOD的面积,分别为S1、S2、S3和S4.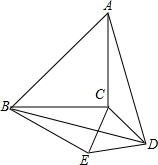 如图,以等腰直角三角形ABC的斜边AB为边向顶点C的同侧等边△ABD,连接DC,以DC为边作等边△DCE,B、E在CD的同侧,若BC=2,则BE=
如图,以等腰直角三角形ABC的斜边AB为边向顶点C的同侧等边△ABD,连接DC,以DC为边作等边△DCE,B、E在CD的同侧,若BC=2,则BE= 如图,过矩形ABCD顶点A作AE⊥BD于E,连接EC,已知S△ABE+S△DEC=15,tan∠BAE=
如图,过矩形ABCD顶点A作AE⊥BD于E,连接EC,已知S△ABE+S△DEC=15,tan∠BAE=