题目内容
 如图,△ABC内的线段BD、CE相交于点O,已知OB=OD,OC=2OE,设△BOE、△BOC、△COD和四边形AEOD的面积,分别为S1、S2、S3和S4.
如图,△ABC内的线段BD、CE相交于点O,已知OB=OD,OC=2OE,设△BOE、△BOC、△COD和四边形AEOD的面积,分别为S1、S2、S3和S4.(1)求S1:S3的值;
(2)如果S2=2,求S4的值.
考点:三角形的面积
专题:
分析:(1)根据△BOC的边OB和△DOC的边OD上的高相同得出
=
,求出S2=S3,同理求出S2=2S1,即可得出答案;
(2)连接OA,求出S1=1,S3=2,设△AOD的面积为x,得出△BAO的面积为x,△AOE的面积为x-1,求出S△AOC=2S△AOE,得出方程x+2=2(x-1),求出方程的解即可.
| S2 |
| S3 |
| OB |
| OD |
(2)连接OA,求出S1=1,S3=2,设△AOD的面积为x,得出△BAO的面积为x,△AOE的面积为x-1,求出S△AOC=2S△AOE,得出方程x+2=2(x-1),求出方程的解即可.
解答:解:(1)∵△BOC的边OB和△DOC的边OD上的高相同,设此高为h,
∴
=
=
,
∵OB=OD,
∴S2=S3,
∵△BOE的边OE和△BOC的边OC上的高相同,设此高为a,
∴
=
=
,
∵OC=2OE,
∴S2=2S1,
∴S3=2S1,
∴S1:S3=1:2.
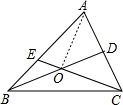 (2)连接OA,
(2)连接OA,
∵S2=2,
∴S1=1,S3=2,
设△AOD的面积为x,
∵OB=OD,
∴△BAO的面积为x,
∴△AOE的面积为x-1,
∵OC=2OE,
∴S△AOC=2S△AOE,
∴x+2=2(x-1),
解得:x=4,
∴S4=4+4-1=7.
∴
| S2 |
| S3 |
| ||
|
| OB |
| OD |
∵OB=OD,
∴S2=S3,
∵△BOE的边OE和△BOC的边OC上的高相同,设此高为a,
∴
| S1 |
| S2 |
| ||
|
| OE |
| OC |
∵OC=2OE,
∴S2=2S1,
∴S3=2S1,
∴S1:S3=1:2.
 (2)连接OA,
(2)连接OA,∵S2=2,
∴S1=1,S3=2,
设△AOD的面积为x,
∵OB=OD,
∴△BAO的面积为x,
∴△AOE的面积为x-1,
∵OC=2OE,
∴S△AOC=2S△AOE,
∴x+2=2(x-1),
解得:x=4,
∴S4=4+4-1=7.
点评:本题考查了三角形面积的应用,注意:等高的两三角形的面积之比等于对应的边之比,题目比较好,有一定的难度.

练习册系列答案
相关题目
地球绕太阳转动一天通过的路程约是2640000千米,用科学记数法表示为( )
| A、2.64×107 |
| B、2.64×106 |
| C、26.4×105 |
| D、264×104 |
当x>0,y<0时,则x,x+y,x-y中最大的数是( )
| A、x | B、x+y |
| C、x-y | D、以上答案不对 |
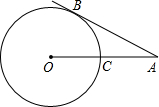 如图,AB切⊙O于B,OA交⊙O于C,∠A=30°,若⊙O半径为3cm,求AO的长.
如图,AB切⊙O于B,OA交⊙O于C,∠A=30°,若⊙O半径为3cm,求AO的长.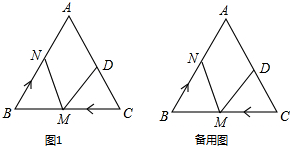 如图,在等边△ABC中,AB=AC=BC=10cm,DC=4cm.如果点M以2cm/秒的速度运动.
如图,在等边△ABC中,AB=AC=BC=10cm,DC=4cm.如果点M以2cm/秒的速度运动. 在如图的网格图中按要求画出图形,并回答问题:
在如图的网格图中按要求画出图形,并回答问题: