题目内容
19.已知二次函数y=ax2+bx+c的图象与x轴交于点(-2,0),(x,0),且1<x1<2,与y轴的正半轴的交点在(0,2)的下方,下列结论正确的是( )①4a-2b+c=0
②a<b<0
③2a+c>0
④2a-b+1>0.
| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②③④ |
分析 ①由函数图象过点(-2,0),将点(-2,0)代入到抛物线解析式即可得知①正确;②结合函数图象与x轴的交点横坐标可以得知抛物线对称轴-$\frac{1}{2}$<-$\frac{b}{2a}$<0,再由抛物线与y轴的交点在y轴正半轴得知a<0,解不等式即可得知②正确;③令ax2+bx+c=0,由根与系数的关系即可得出关于$\frac{c}{a}$的不等式,解不等式得出c与a之间的关系,将其代入2a+c即可得知③正确;④由抛物线与y轴交点坐标的范围可找出c的范围,结合抛物线的图象过点(-2,0),将c换成2即可得知④正确.综上即可得出结论.
解答 解:①∵二次函数y=ax2+bx+c的图象经过点(-2,0),
∴0=4a-2b+c,①正确;
②∵二次函数y=ax2+bx+c的图象与x轴交于点(-2,0),(x,0),且1<x1<2,
∴抛物线的对称轴-$\frac{1}{2}$<x=-$\frac{b}{2a}$<0.
∵抛物线图象与x轴的两交点分别在原点两侧,与y轴的交点在y轴正半轴,
∴抛物线开口向下,即a<0,
∵-$\frac{1}{2}$<-$\frac{b}{2a}$<0,
∴a<b<0,即②正确;
③令ax2+bx+c=0,
则方程的两个解为:1<x1<2,x2=-2,
∴$\frac{c}{a}$=x1•x2,即-4<$\frac{c}{a}$<-2,
又∵a<0,
∴-2a<c<-4a,
∴2a+c>0,即③正确;
④∵抛物线图象与y轴的正半轴的交点在(0,2)的下方
∴c<2,
∵当x=-2时,y=0,即:4a-2b+c=0,
∴4a-2b+2>0,
∴2a-b+1>0,即D正确.
故选D.
点评 本题考查了二次函数图象与系数的关系、根与系数的关系以及解不等式,解题的关键是依据二次函数图象与系数的关系逐条分析4条结论.本题属于基础题,难度不大,解决该题型题目时,熟练利用二次函数图象与系数的关系解决问题是关键.

 阅读快车系列答案
阅读快车系列答案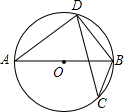 如图,AB是⊙O的直径,CD是⊙O的弦,连接AD、DB、BC,若∠ABD=55°,则∠BCD的度数为( )
如图,AB是⊙O的直径,CD是⊙O的弦,连接AD、DB、BC,若∠ABD=55°,则∠BCD的度数为( )| A. | 65° | B. | 55° | C. | 45° | D. | 35° |
| A. | $\sqrt{4}$=±2 | B. | 2+$\sqrt{3}$=2$\sqrt{3}$ | C. | 2x-2=$\frac{1}{2{x}^{2}}$ | D. | (-a3)2=a6 |
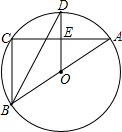 如图,AB是△ABC的外接圆⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,BC=5,AE=6,则DE的长为( )
如图,AB是△ABC的外接圆⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,BC=5,AE=6,则DE的长为( )| A. | 4$\sqrt{2}$ | B. | 3$\sqrt{3}$ | C. | 4 | D. | $\frac{7}{2}$ |
 如图是正方体的一个平面展开图,如果原正方体上“友”所在的面为前面,则“信”与“国”所在的面分别位于( )
如图是正方体的一个平面展开图,如果原正方体上“友”所在的面为前面,则“信”与“国”所在的面分别位于( )| A. | 上,下 | B. | 右,后 | C. | 左,右 | D. | 左,后 |