题目内容
 如图,四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC和CD于点P,Q,则BP:PQ:QR=
如图,四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC和CD于点P,Q,则BP:PQ:QR=考点:相似三角形的判定与性质,平行四边形的性质
专题:
分析:利用平行四边形的性质得到平行,可得到PB=PR,
=
,且DR=RE,代入可得到QR和PQ之间的关系,结合BP=PR=3PQ,可得到答案.
| PC |
| RE |
| 1 |
| 2 |
解答:解:∵四边形ABCD和四边形ACED都是平行四边形,
∴BC=AD=CE,AC∥DE,
∴PB=PR,
=
,
又∵PC∥DR,
∴△PCQ∽△RDQ,
又∵点R是DE中点,
∴DR=RE,
∴
=
=
=
,
∴QR=2PQ,
又∵BP=PR=PQ+QR=3PQ,
∴BP:PQ:QR=3:1:2,
故答案为:3:1:2.
∴BC=AD=CE,AC∥DE,
∴PB=PR,
| PC |
| RE |
| 1 |
| 2 |
又∵PC∥DR,
∴△PCQ∽△RDQ,
又∵点R是DE中点,
∴DR=RE,
∴
| PQ |
| QR |
| PC |
| DR |
| PC |
| RE |
| 1 |
| 2 |
∴QR=2PQ,
又∵BP=PR=PQ+QR=3PQ,
∴BP:PQ:QR=3:1:2,
故答案为:3:1:2.
点评:本题主要考查平行线分线段成比例的性质及平行四边形的性质,由条件得到QR=2PQ、BP=3PQ是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
从一个装有30个红球,20个蓝球,10个白球的布袋中随机摸出一种球的概率为
,则这球的颜色是( )
| 1 |
| 3 |
| A、红色 | B、蓝色 |
| C、白色 | D、以上都有可能 |
 如图,为了测量山坡的护坡石坝与地面的倾斜角α,把一根长为4.5m的竹竿AC斜靠在石坝旁,量出竿长1米时它离地面的高度为0.6m,又量得竿顶与坝脚的距离BC=2.8m,这样∠α就可以计算出来了,请你算一算.
如图,为了测量山坡的护坡石坝与地面的倾斜角α,把一根长为4.5m的竹竿AC斜靠在石坝旁,量出竿长1米时它离地面的高度为0.6m,又量得竿顶与坝脚的距离BC=2.8m,这样∠α就可以计算出来了,请你算一算. 如图,点A,B在数轴上,它们所对应的数分别是-5,
如图,点A,B在数轴上,它们所对应的数分别是-5,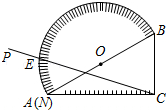 如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第27秒,点E在量角器上对应的读数是
如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第27秒,点E在量角器上对应的读数是
 如图所示,两条直线l1,l2的交点坐标可以看作方程组
如图所示,两条直线l1,l2的交点坐标可以看作方程组