题目内容
20.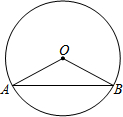 如图,⊙O的半径长为13cm,圆内一弦AB的长为24cm,求圆心O到弦AB的距离.
如图,⊙O的半径长为13cm,圆内一弦AB的长为24cm,求圆心O到弦AB的距离.
分析 过O作弦AB的垂线OF,设垂足为C,在构造的Rt△OAF中,由垂径定理可得AF的长,圆的半径已知,即可由勾股定理求得OF的值,即圆心O到弦AB的距离.
解答 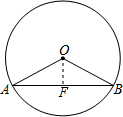 解:过圆心O作OF⊥AB于点F,则AF=$\frac{1}{2}$AB=12cm;
解:过圆心O作OF⊥AB于点F,则AF=$\frac{1}{2}$AB=12cm;
Rt△OAF中,AF=12cm,OA=13cm,由勾股定理得:
OF=$\sqrt{O{A}^{2}-A{F}^{2}}$=5cm,
即圆心O到弦AB的距离是5cm.
点评 本题考查了勾股定理、垂径定理.此题涉及圆中求弦心距的问题,此类在圆中涉及弦长、半径的计算的问题,常把半弦长、半径、圆心到弦距离转换到同一直角三角形中,然后通过直角三角形予以求解.

练习册系列答案
相关题目
12.下列方程中,关于x的一元二次方程是( )
| A. | ax2+bx+c=0 | B. | $\frac{1}{{x}^{2}}+\frac{1}{x}$-2=0 | C. | x2+2x-1=0 | D. | x2+2x=x2-1 |
 已知:如图,DE⊥AC,BF⊥AC,AD=BC,DE=BF.
已知:如图,DE⊥AC,BF⊥AC,AD=BC,DE=BF.