Question

【题目】在平面直角坐标系中，为原点，点，点，点，把绕点顺时针旋转（旋转角为锐角），得，、、旋转后的对应点分别为、、，、分别与轴、轴交于点、．

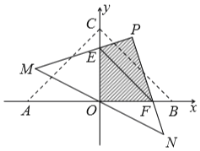
（1）求四边形的面积；

（2）设，，用含的式子表示；

（3）设点关于原点的对称点为，当的值最小时，求的坐标．（直接写出结果）

Answer 1

【答案】（1）2；（2）；（3）

【解析】

（1）连接OP，有△MNP是等腰直角三角形，证明，即可得到

故即为所求．

（2）由，，根据，=S四边形OEPF-，即可求出S和m的关系式．

（3）通过图象观察当旋转角为45°时，值最小，根据旋转的性质，即可求出Q点坐标．

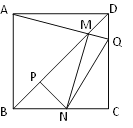
（1）连接OP

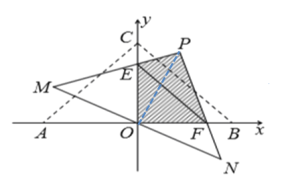
∵点，点，点

∴△ABC是等腰直角三角形，且O是斜边AB的中点

∴根据旋转的性质，有△MNP是等腰直角三角形

∴OM=OP，∠OME=∠OPF=45°

∵∠MOP=90°，∠EOF=90°

∴∠MOE=∠POF

∴

∴

∴

故答案为：2

（2）∵

∴

∵

∴

∴=S四边形OEPF-=

故答案为：

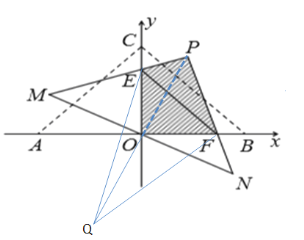
（3）由图可知当旋转角为45°时，值最小

∵Q点是P点关于原点对称的点

∵OP=2

设Q点横纵坐标均为a

∴2a2=4

∴a=

∴

故答案为：