Question

【题目】在中，，，，点、分别在边、上．如果为中点，且，那么的长度为__________．

Answer 1

【答案】5或1.4

【解析】

根据已知比例式先求出DE的长，再分两种情况：①E为BC的中点，可直接得出AE的长；②点E在靠近点A的位置，过点D作DF⊥AC于点F，证明△ADF∽△ACB，得出，从而可得出DF的长，再分别根据勾股定理得出AF，EF的长，从而可得出结果．

解：∵在中，根据勾股定理得，AC=，

又D是AB的中点，∴AD=AB=4，

∵，

∴，∴DE=3．

分以下两种情况：

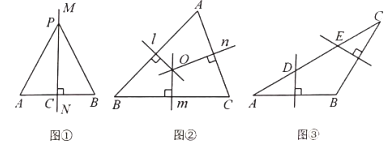
①当点E在如图①所示的位置时，即点E为AC的中点时，DE=BC=3，

故此时AE=AC=5；

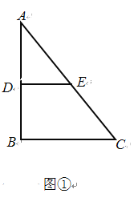
②点E在如图②所示的位置时，DE=3，过点D作DF⊥AC于点F，

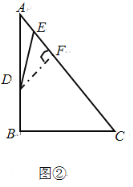
∵∠AFD=∠B=90°，∠A=∠A，

∴△ADF∽△ACB，

∴，即，∴DF=2.4．

∴在Rt△ADF中，AF=，

在Rt△DEF中，EF=，

∴AE=AF-EF=1.4．

综上所述，AE的长为5或1.4．

故答案为：5或1.4．