题目内容
4.探索:(x-1)(x+1)=x2-1(x-1)(x2+x+1)=x3-1(x-1)(x3+x2+x+1)=x4-1(x-1)(x4+x3+x2+x+1)=x5-1,则26+25+24+23+22+2+1=127,32016+32015+32014+…+32+3+1=$\frac{{3}^{2017}-1}{2}$.分析 将原式变形为(2-1)(26+25+24+23+22+2+1),利用(x-1)(xn+xn-1+xn-2+…+x+1)=xn+1-1,进一步计算可得;同理32016+32015+32014+…+32+3+1=$\frac{1}{2}$×(3-1)(32016+32015+32014+…+32+3+1)继而得出答案.
解答 解:由题意知(x-1)(xn+xn-1+xn-2+…+x+1)=xn+1-1,
则26+25+24+23+22+2+1=(2-1)(26+25+24+23+22+2+1)=27-1=127,
32016+32015+32014+…+32+3+1=$\frac{1}{2}$×(3-1)(32016+32015+32014+…+32+3+1)=$\frac{{3}^{2017}-1}{2}$,
故答案为:127,$\frac{{3}^{2017}-1}{2}$.
点评 本题主要考查了数字的变化规律,根据已知等式得出(x-1)(xn+xn-1+xn-2+…+x+1)=xn+1-1并将待求式子灵活变形得以运用规律是解题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
15.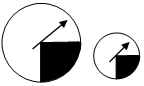 有大小两个转盘,其中黑色区域都是中心角为90°的扇形,为了探究指针落在黑色区域的频率,甲乙两人分别转动两转盘,记录下表(A:指针落在大转盘的黑色区域频数;B:大转盘中的频率;C:指针落在小转盘的黑色区域频数;D:小转盘中相应频率)
有大小两个转盘,其中黑色区域都是中心角为90°的扇形,为了探究指针落在黑色区域的频率,甲乙两人分别转动两转盘,记录下表(A:指针落在大转盘的黑色区域频数;B:大转盘中的频率;C:指针落在小转盘的黑色区域频数;D:小转盘中相应频率)
(1)将B、D两空格填写完整;
(2)分别绘出指针落在大小转盘中黑色区域的频率折线图;
(3)比较25次与50次的大小频率之差及200与225次之间大小转盘两频率之差;
(4)从(3)中频率之差及折线统计图中的变化趋势,你能总结出什么规律?
 有大小两个转盘,其中黑色区域都是中心角为90°的扇形,为了探究指针落在黑色区域的频率,甲乙两人分别转动两转盘,记录下表(A:指针落在大转盘的黑色区域频数;B:大转盘中的频率;C:指针落在小转盘的黑色区域频数;D:小转盘中相应频率)
有大小两个转盘,其中黑色区域都是中心角为90°的扇形,为了探究指针落在黑色区域的频率,甲乙两人分别转动两转盘,记录下表(A:指针落在大转盘的黑色区域频数;B:大转盘中的频率;C:指针落在小转盘的黑色区域频数;D:小转盘中相应频率)| 次数 | 25 | 50 | 75 | 100 | 125 | 150 | 175 | 200 | 225 |
| A | 8 | 15 | 21 | 26 | 32 | 36 | 44 | 51 | 57 |
| B | 0.32 | 0.30 | 0.28 | 0.26 | 0.256 | 0.24 | 0.251 | 0.255 | 0.253 |
| C | 8 | 13 | 21 | 26 | 32 | 37 | 43 | 49 | 55 |
| D | 0.32 | 0.26 | 0.28 | 0.26 | 0.256 | 0.247 | 0.246 | 0.245 | 0.244 |
(2)分别绘出指针落在大小转盘中黑色区域的频率折线图;
(3)比较25次与50次的大小频率之差及200与225次之间大小转盘两频率之差;
(4)从(3)中频率之差及折线统计图中的变化趋势,你能总结出什么规律?
13.若x2+ax+9=(x-3)2,则a的值为( )
| A. | 3 | B. | ±3 | C. | -6 | D. | ±6 |
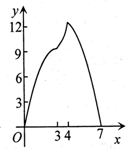
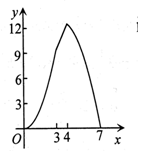
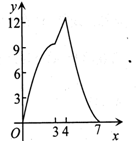
 如图,点A(0,3),B(4,0),以AB为边作正方形ABCD,点F是射线OB上一动点,过点F作EF⊥x轴交正方形ABCD于P,Q两点,设OF=x,△APQ的面积为y,下列图象中,能表示y与x之间的函数关系的图象大致是( )
如图,点A(0,3),B(4,0),以AB为边作正方形ABCD,点F是射线OB上一动点,过点F作EF⊥x轴交正方形ABCD于P,Q两点,设OF=x,△APQ的面积为y,下列图象中,能表示y与x之间的函数关系的图象大致是( )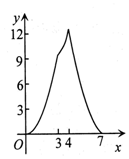
 如图,直线AC与直线DE相交于点O,若∠BOC=35°,BO⊥DE,垂足为O,则∠AOD=55度.
如图,直线AC与直线DE相交于点O,若∠BOC=35°,BO⊥DE,垂足为O,则∠AOD=55度.