题目内容
3．
在矩形ABCD中，AB=12，AD=5，以点A为圆心，r为半径作圆．（1）若矩形ABCD的顶点至多有两个在⊙A内，求r的取值范围；
（2）若矩形ABCD的顶点至少有两个在⊙A内，求r的取值范围．
分析 （1）根据点与圆的位置关系，点B在圆外，可得答案；
（2）根据点与圆的位置关系，点D在圆内，可得答案．
解答 解：（1）当恰好有三个顶点在圆内时，即此时以AB为半径，r=12，
矩形ABCD的顶点至多有两个在⊙A内，0＜r＜12；
（2）当恰好有两个顶点在圆内时，即此时以AO为半径，r=5，
矩形ABCD的顶点至少有两个在⊙A内，r的取值范围是r＞5．
点评 本题考查了对点与圆的位置关系，关键要记住若半径为r，点到圆心的距离为d，则有：当d＞r时，点在圆外；当d=r时，点在圆上，当d＜r时，点在圆内．
练习册系列答案
相关题目
8．下列式子中，不成立的是（ ）
| A． | $\sqrt{2}$cos45°=2sin30° | B． | tan30°•sin60°=sin245° | ||
| C． | cos45°-sin45°=0 | D． | sin（30°+45°）=sin30°+sin45° |
如图，在梯形ABCD中，AD∥BC，EF∥BC，EF分别交AB，CD，AC于点E、F、G．若$\frac{CF}{FD}$=$\frac{2}{3}$，则$\frac{BE}{EA}$=$\frac{2}{3}$，$\frac{CG}{CA}$=$\frac{2}{5}$，$\frac{AG}{AC}$=$\frac{3}{5}$，$\frac{AB}{EB}$=$\frac{5}{2}$．
15．
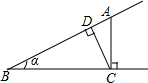如图，点A为∠α边上任意一点，作AC⊥BC于点C，CD⊥AB于点D，下列用线段比表示sinα的值，错误的是（ ）
如图，点A为∠α边上任意一点，作AC⊥BC于点C，CD⊥AB于点D，下列用线段比表示sinα的值，错误的是（ ）| A． | $\frac{CD}{BC}$ | B． | $\frac{AC}{AB}$ | C． | $\frac{AD}{AC}$ | D． | $\frac{CD}{AC}$ |
12．若-2a2b4与5an-2b2m是同类项，则mn的值是（ ）
| A． | 2 | B． | 4 | C． | 8 | D． | 16 |
如图，坐标系中正方形网格的单位长度为1，抛物线y1=-$\frac{1}{2}{x^2}$+3向下平移2个单位后得抛物线y2，则阴影部分的面积S=4．