题目内容
20. 叙述三角形的中位线定理,并结合图形进行证明.
叙述三角形的中位线定理,并结合图形进行证明.定理:
证明:
分析 作出图形,然后写出已知、求证,延长EF到D,使FD=EF,利用“边角边”证明△AEF和△CDF全等,根据全等三角形对应边相等可得AE=CD,全等三角形对应角相等可得∠D=∠AEF,再求出CE=CD,根据内错角相等,两直线平行判断出AB∥CD,然后判断出四边形BCDE是平行四边形,根据平行四边形的性质可得DE∥BC,DE=BC.
解答 解:定理:三角形的中位线平行于第三边并且等于第三边的一半.
已知:△ABC中,点E、F分别是AB、AC的中点,
求证:EF=$\frac{1}{2}$AB,EF∥AB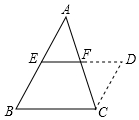 ,
,
证明:如图,延长EF到D,使FD=EF,连接CD,
∵点F是AC的中点,
∴AF=CF,
在△AEF和△CDF中,
$\left\{\begin{array}{l}{AF=FC}\\{∠AFE=∠CFD}\\{EF=FD}\end{array}\right.$,
∴△AEF≌△CDF(SAS),
∴AE=CD,∠D=∠AEF,
∴AB∥CD,
∵点E是AB的中点,
∴AE=BE,
∴BE=CD,
∴BECD,
∴四边形BCDE是平行四边形,
∴DE∥BC,DE=BC,
∴DE∥BC且DE=$\frac{1}{2}$BC.
点评 本题考查了三角形的中位线定理的证明,关键在于作辅助线构造成全等三角形和平行四边形,文字叙述性命题的证明思路和方法需熟练掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.一组数据4,5,7,7,8,6的中位数和众数分别是( )
| A. | 7,7 | B. | 7,6.5 | C. | 6.5,7 | D. | 5.5,7 |
15.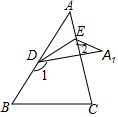 如图,△ABC中,D、E分别为AB、AC上两点,将△ABC沿直线DE折叠,使得点A落在△ABC右侧的点A1处,则∠A、∠1、∠2之间满足的关系式是( )
如图,△ABC中,D、E分别为AB、AC上两点,将△ABC沿直线DE折叠,使得点A落在△ABC右侧的点A1处,则∠A、∠1、∠2之间满足的关系式是( )
 如图,△ABC中,D、E分别为AB、AC上两点,将△ABC沿直线DE折叠,使得点A落在△ABC右侧的点A1处,则∠A、∠1、∠2之间满足的关系式是( )
如图,△ABC中,D、E分别为AB、AC上两点,将△ABC沿直线DE折叠,使得点A落在△ABC右侧的点A1处,则∠A、∠1、∠2之间满足的关系式是( )| A. | ∠A=∠1-∠2 | B. | ∠A=$\frac{1}{2}$∠1-∠2 | C. | ∠A=∠1-2∠2 | D. | 2∠A=∠1-∠2 |
9.在平面直角坐标系中,将点A(-1,2)向右平移3个单位长度,再向下平移1个单位长度得到点B,则点B的坐标为( )
| A. | (2,2) | B. | (2,1) | C. | (2,3) | D. | (-4,3) |
10.为了了解某校七年级期末考试数学科各分数段成绩分布情况,从参加考试的900名学生中抽取300名考生的期末数学成绩进行统计分析,在这个问题中,样本是( )
| A. | 300 | |
| B. | 被抽取的300名学生 | |
| C. | 被抽取的300名考生的期末数学成绩 | |
| D. | 某校七年级期末900名学生的数学成绩 |
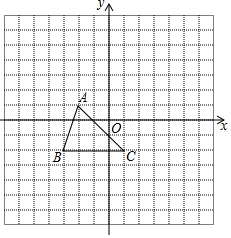 已知:如图,把△A′B′C′向下平移3个单位长度,再向左平移2个单位长度,得到△ABC.
已知:如图,把△A′B′C′向下平移3个单位长度,再向左平移2个单位长度,得到△ABC. 如图,Rt△ABC中,∠C=90°,BC=3,点O在AB上,OB=2,以OB为半径的⊙O与AC相切于点D,交BC于点E,求弦BE的长.
如图,Rt△ABC中,∠C=90°,BC=3,点O在AB上,OB=2,以OB为半径的⊙O与AC相切于点D,交BC于点E,求弦BE的长.