题目内容
8. 如图,Rt△ABC中,∠C=90°,BC=3,点O在AB上,OB=2,以OB为半径的⊙O与AC相切于点D,交BC于点E,求弦BE的长.
如图,Rt△ABC中,∠C=90°,BC=3,点O在AB上,OB=2,以OB为半径的⊙O与AC相切于点D,交BC于点E,求弦BE的长.
分析 连接OD,首先证明四边形OFCD是矩形,从而得到BF的长,然后利用垂径定理求得BE的长即可.
解答  解:连接OD,作OF⊥BE于点F.
解:连接OD,作OF⊥BE于点F.
∴BF=$\frac{1}{2}$BE,
∵AC是圆的切线,
∴OD⊥AC,
∴∠ODC=∠C=∠OFC=90°,
∴四边形ODCF是矩形,
∵OD=OB=FC=2,BC=3,
∴BF=BC-FC=BC-OD=3-2=1,
∴BE=2BF=2.
点评 本题考查了切线的性质、勾股定理及垂径定理的知识,解题的关键是能够利用切线的性质构造矩形形,难度不大.

练习册系列答案
相关题目
13.下列图形可由平移得到的是( )
| A. |  | B. |  | C. |  | D. |  |
17.在平面直角坐标系中,把直线y=x-2向左平移2个单位长度后,其直线解析式为( )
| A. | y=x+1 | B. | y=x-1 | C. | y=x | D. | y=x-2 |
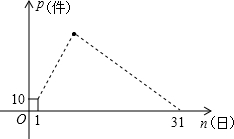 3月份,某品牌衬衣正式上市销售,3月1日的销售量为10件,3月2日的销售量为35件,以后每天的销售量比前一天多25件,直到日销售量达到最大后,销售量开始逐日下降,至此,每天的销售量比前一天少15件,直到3月31日销售量为0.设该品牌衬衣的日销量为p(件),销售日期为n(日),p与n之间的关系如图所示.
3月份,某品牌衬衣正式上市销售,3月1日的销售量为10件,3月2日的销售量为35件,以后每天的销售量比前一天多25件,直到日销售量达到最大后,销售量开始逐日下降,至此,每天的销售量比前一天少15件,直到3月31日销售量为0.设该品牌衬衣的日销量为p(件),销售日期为n(日),p与n之间的关系如图所示. 如图:
如图: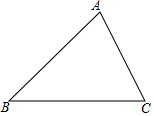 叙述三角形的中位线定理,并结合图形进行证明.
叙述三角形的中位线定理,并结合图形进行证明. 如图所示是长方体的平面展开图,设AB=x,若AD=4x,AN=3x.
如图所示是长方体的平面展开图,设AB=x,若AD=4x,AN=3x.