题目内容
12.计算:($\overrightarrow m$-3$\overrightarrow n$)-$\frac{1}{2}$($\overrightarrow m$+2$\overrightarrow n$)=$\frac{1}{2}\overrightarrow m-4\overrightarrow n$.分析 根据平面向量的加法计算法则和向量数乘的结合律进行计算.
解答 解::($\overrightarrow m$-3$\overrightarrow n$)-$\frac{1}{2}$($\overrightarrow m$+2$\overrightarrow n$)=$\overrightarrow m$-3$\overrightarrow n$-$\frac{1}{2}$$\overrightarrow m$-$\frac{1}{2}$×2$\overrightarrow n$)=$\frac{1}{2}\overrightarrow m-4\overrightarrow n$.
故答案是:$\frac{1}{2}\overrightarrow m-4\overrightarrow n$.
点评 本题考查了平面向量,熟记计算法则即可解题,属于基础题型.

练习册系列答案
相关题目
2.若-3x2ny3与2x4ym是同类项,则|m-n|( )
| A. | -1 | B. | 7 | C. | 1 | D. | 0 |
2.下列抛物线中,与抛物线y=x2-2x+4具有相同对称轴的是( )
| A. | y=4x2+2x+1 | B. | y=2x2-4x+1 | C. | y=2x2-x+4 | D. | y=x2-4x+2 |
 请写出图中所有的邻补角,同位角及内错角.
请写出图中所有的邻补角,同位角及内错角.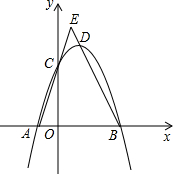 如图,已知抛物线y=-x2+bx+3与x轴相交于点A和点B(点A在点B的左侧),与y轴交于点C,且OB=OC,点D是抛物线的顶点,直线AC和BD交于点E.
如图,已知抛物线y=-x2+bx+3与x轴相交于点A和点B(点A在点B的左侧),与y轴交于点C,且OB=OC,点D是抛物线的顶点,直线AC和BD交于点E.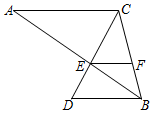 如图,已知AC∥BD,AB和CD相交于点E,AC=6,BD=4,F是BC上一点,S△BEF:S△EFC=2:3.
如图,已知AC∥BD,AB和CD相交于点E,AC=6,BD=4,F是BC上一点,S△BEF:S△EFC=2:3.