如图.正方形ABCD的边长为4.点E是BC的中点.AF=3BF.点P为对角线AC上一动点.则FP+EP的最小值是( )A．$\sqrt{15}$B．$\sqrt{17}$C．5D．4$\sqrt{2}$ 题目和参考答案——青夏教育精英家教网—

题目内容

17．

如图，正方形ABCD的边长为4，点E是BC的中点，AF=3BF，点P为对角线AC上一动点，则FP+EP的最小值是（　　）

A．

$\sqrt{15}$

B．

$\sqrt{17}$

C．

D．

4$\sqrt{2}$

分析首先作点E关于AC的对称点M，连接FM，过点F作FN⊥CD于点N，由四边形ABCD是正方形，可得M是CD的中点，PM是FP+EP的最小值，然后利用勾股定理求解即可求得答案．

解答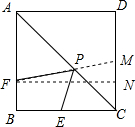解：作点E关于AC的对称点M，连接FM，过点F作FN⊥CD于点N，
∵四边形ABCD是正方形，
∴M是CD的中点，PM是FP+EP的最小值，
∵正方形ABCD的边长为4，点E是BC的中点，AF=3BF，
∴BF=$\frac{1}{4}$AB=1，CM=CE=$\frac{1}{2}$BC=2，
∵四边形BCNP是矩形，
∴FN=BC=4，CN=BF=1，
∴MN=CM-CN=1，
∴FM=$\sqrt{F{N}^{2}+M{N}^{2}}$=$\sqrt{17}$．
即FP+EP的最小值是：$\sqrt{17}$．
故选B．

点评此题考查了最短路径问题以及正方形的性质．注意准确找到点P的位置是解此题的关键．

练习册系列答案

相关题目

7．化简$\sqrt{8}$的结果是（　　）

8．甲、乙二人做某种零件，已知甲每小时比乙多做6个，甲做90个所用的时间与乙做60个所用的时间相等，若设乙每小时做x个，则可列方程（　　）

A．

$\frac{90}{x}=\frac{60}{x-6}$

B．

$\frac{90}{x-6}=\frac{60}{x}$

C．

$\frac{90}{x+6}=\frac{60}{x}$

D．

$\frac{90}{x}=\frac{60}{x+6}$

5．在方差的计算公式${S^2}=\frac{1}{10}[{{{（{{x_1}-20}）}^2}+{{（{{x_2}-20}）}^2}+…+{{（{{x_{10}}-20}）}^2}}]$中，数字10和20分别表示的意义应当是（　　）

	A．	数据的个数和方差		B．	数据的平均数和数据的个数
	C．	数据的个数和数据的平均数		D．	数据的方差和数据的平均数

12．

在平行四边形ABCD中，对角线AC和BD交于点O，E是CD的中点，连接OE，若AD=5，CD=4，则OE的长为（　　）

	A．	早上太阳从西方升起
	B．	将油滴入水中，油会浮在水面上
	C．	抛出的石头会下落
	D．	掷一枚骰子，向上一面的数字是偶数

如图1，已知点A（a，0），B（0，b），且a、b满足，?ABCD的边AD与y轴交于点E，且E为AD中点，双曲线y=经过C、D两点．
（1）求k的值；
（2）点P在双曲线y= 上，点Q在y轴上，若以点A、B、P、Q为顶点的四边形是平行四边形，试求满足要求的所有点P、Q的坐标；
（3）以线段AB为对角线作正方形AFBH（如图3），点T是边AF上一动点，M是HT的中点，MN⊥HT，交AB于N，当T在AF上运动时，的值是否发生改变？若改变，求出其变化范围；若不改变，请求出其值，并给出你的证明．