Question

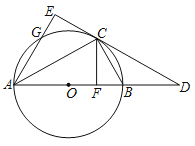
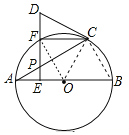
【题目】如图，AB是⊙O的直径，DC为⊙O的切线，DE⊥AB，垂足为点E，交⊙O于点F，弦AC交DE于点P，连接CF．

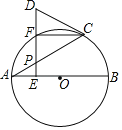
（1）求证：∠DPC＝∠PCD；

（2）若AP＝2，填空：

①当∠CAB＝　 　时，四边形OBCF是菱形；

②当AC＝2AE时，OB＝　 　．

Answer 1

【答案】（1）见解析；（2）①30°，②2

【解析】

（1）由切线的性质和等腰三角形的性质可得∠CAO=∠ACO，∠DEA=∠OCD=90°，可得∠DCA=∠APE=∠DPC；
（2）①由菱形的性质可得OB=BC，可证△OBC是等边三角形，即可求解；
②由圆周角定理可得∠ACB=90°=∠AEP，通过证明△APE∽△ABC，由相似三角形的性质可求解．

（1）如图，连接OC，OF，BC，

∵OA＝OC，

∴∠CAO＝∠ACO，

∵DC为⊙O的切线，

∴OC⊥DC，且DE⊥AB，

∴∠DEA＝∠OCD＝90°，

∴∠CAO+∠APE＝90°，∠ACO+∠DCA＝90°

∴∠DCA＝∠APE＝∠DPC，

（2）①当∠CAB＝30°时，四边形OBCF是菱形；

若四边形OBCF是菱形，

∴OB＝BC，且OB＝OC，

∴△OBC是等边三角形，

∴∠COB＝60°

∵AO＝CO，

∴∠CAB＝30°，

∴当∠CAB＝30°时，四边形OBCF是菱形；

②∵AB是直径，

∴∠ACB＝90°＝∠AEP，且∠CAB＝∠PAE，

∴△APE∽△ABC，

∴，且AC＝2AE

∴AB＝4，

∵AB＝2OB

∴OB＝2

故答案为：30°，2