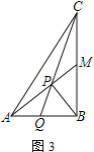
题目内容
【题目】已知⊙![]() 是△
是△![]() 的外接圆,
的外接圆,![]() 是⊙
是⊙![]() 的直径,
的直径,![]() 是
是![]() 延长线上的一点,
延长线上的一点,![]() 交
交![]() 的延长线于
的延长线于![]() ,交⊙
,交⊙![]() 于
于![]() ,
,![]() 于
于![]() ,点
,点![]() 是弧
是弧![]() 的中点.
的中点.
⑴求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
⑵若![]() 是一元二次方程
是一元二次方程![]() 的两根,求
的两根,求![]() 和
和![]() 的长.
的长.
【答案】(1)见解析;(2)CE=![]() ,AG=4
,AG=4
【解析】
(1)连接![]() ,由
,由![]() ,
,![]() ,得:
,得:![]() ,从而得:
,从而得:![]() ∥
∥![]() ,进而得到:
,进而得到:![]() ,即可得证;
,即可得证;
(2)易得:![]() ,由CAF~BCF,得:
,由CAF~BCF,得:![]() ,进而得:
,进而得:![]() ,进而求得CE的长,由
,进而求得CE的长,由![]() △
△![]() ≌
≌![]() △
△![]() (HL),得:
(HL),得:![]() ,由
,由![]() △
△![]() ≌
≌![]() △
△![]() (HL),得
(HL),得![]() ,进而求出AG的长.
,进而求出AG的长.
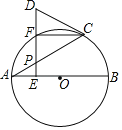
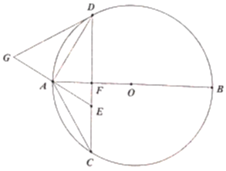
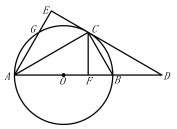
⑴.证明:连接![]() ,如图1,
,如图1,
∵![]() ,
,
∴![]() ,
,
∵点![]() 是弧
是弧![]() 的中点,即
的中点,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ∥
∥![]() ,
,
∴ ![]() ,
,
∵![]() ,
,
∴![]() , 即
, 即![]() ,
,
又∵![]() 是⊙
是⊙![]() 的半径,
的半径,
∴![]() 是⊙
是⊙![]() 的切线.
的切线.
⑵解一元二次方程![]() 的两根为:
的两根为:![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() 是⊙
是⊙![]() 的直径,
的直径,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵∠CAF+∠ACF=90°,∠ACF+∠BCF=90°,
∴∠CAF=∠BCF,
∴CAF~BCF,
∴![]() ,即:
,即:![]() ,
,
∴![]() ,
,
∵![]() ,且
,且![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() △
△![]() ≌
≌![]() △
△![]() (HL),
(HL),
∴![]() ,
,
连接![]() ,如图2,
,如图2,
∵点![]() 是弧
是弧![]() 的中点,即
的中点,即![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() △
△![]() ≌
≌![]() △
△![]() (HL),
(HL),
∴![]() ,
,
∴![]() .
.

图1 图2

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
【题目】在![]() 中,
中,![]() ,
,![]() 为
为![]() 边上一动点(点
边上一动点(点![]() 与点
与点![]() 不重合),联结
不重合),联结![]() ,过点
,过点![]() 作
作![]() 交边
交边![]() 于点
于点![]() .
.
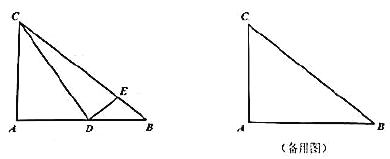
(1)如图,当![]() 时,求
时,求![]() 的长;
的长;
(2)设![]() ,求
,求![]() 关于
关于![]() 的函数解析式并写出函数定义域;
的函数解析式并写出函数定义域;
(3)把![]() 沿直线
沿直线![]() 翻折得
翻折得![]() ,联结
,联结![]() ,当
,当![]() 是等腰三角形时,直接写出
是等腰三角形时,直接写出![]() 的长.
的长.