题目内容
14.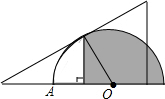 如图,将一块含30°角的直角三角板和半圆量角器按如图的方式摆放,使斜边与半圆相切.若半径OA=2,则图中阴影部分的面积为$\frac{4π}{3}$+$\frac{\sqrt{3}}{2}$.(结果保留π)
如图,将一块含30°角的直角三角板和半圆量角器按如图的方式摆放,使斜边与半圆相切.若半径OA=2,则图中阴影部分的面积为$\frac{4π}{3}$+$\frac{\sqrt{3}}{2}$.(结果保留π)
分析 图中阴影部分的面积=扇形BOD的面积+△BOC的面积.
解答  解:∵斜边与半圆相切,点B是切点,
解:∵斜边与半圆相切,点B是切点,
∴∠EBO=90°.
又∵∠E=30°,
∴∠EBC=60°.
∴∠BOD=120°,
∵OA=OB=2,
∴OC=$\frac{1}{2}$OB=1,BC=$\sqrt{3}$.
∴S阴影=S扇形BOD+S△BOC=$\frac{120π×{2}^{2}}{360}$+$\frac{1}{2}$×1×$\sqrt{3}$=$\frac{4π}{3}$+$\frac{\sqrt{3}}{2}$.
故答案是:$\frac{4π}{3}$+$\frac{\sqrt{3}}{2}$.
点评 本题考查了切线的性质,扇形面积的计算.此题利用了“分割法”求得阴影部分的面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.来宾市辖区面积约为13400平方千米,这一数字用科学记数法表示为( )
| A. | 1.34×102 | B. | 1.34×103 | C. | 1.34×104 | D. | 1.34×105 |
9.老师想知道学生每天上学路上要花多少时间,于是让大家将每天来校的单程时间写在纸上用于统计.下面是全班30名学生单程所花时间(单位:分)与对应人数(单位:人)的统计表,则关于这30名学生单程所花时间的数据,下列结论正确的是( )
| 单程所花时间 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 45 |
| 人数 | 3 | 3 | 6 | 12 | 2 | 2 | 1 | 1 |
| A. | 众数是12 | B. | 平均数是18 | C. | 极差是45 | D. | 中位数是20 |
19.下列运算正确的是( )
| A. | 3a2-2a2=1 | B. | (a2)3=a5 | C. | a2•a4=a6 | D. | (3a)2=6a2 |
 已知⊙O是以AB为直径的△ABC的外接圆,OD∥BC交⊙O于点D,交AC于点E,连接AD、BD,BD交AC于点F.
已知⊙O是以AB为直径的△ABC的外接圆,OD∥BC交⊙O于点D,交AC于点E,连接AD、BD,BD交AC于点F. 如图,从一个建筑物的A处测得对面楼BC的顶部B的仰角为32°,底部C的俯角为45°,观测点与楼的水平距离AD为31m,则楼BC的高度约为50m(结果取整数).(参考数据:sin32°≈0.5,cos32°≈0.8,tan32°≈0.6)
如图,从一个建筑物的A处测得对面楼BC的顶部B的仰角为32°,底部C的俯角为45°,观测点与楼的水平距离AD为31m,则楼BC的高度约为50m(结果取整数).(参考数据:sin32°≈0.5,cos32°≈0.8,tan32°≈0.6)