题目内容
18.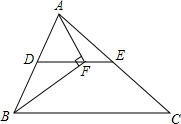 如图,在△ABC中,D为AB的中点,E为AC的中点,F是DE上一点,且AF⊥BF,若AB=10,BC=16,则线段EF的长为( )
如图,在△ABC中,D为AB的中点,E为AC的中点,F是DE上一点,且AF⊥BF,若AB=10,BC=16,则线段EF的长为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 延长AF交BC于H,根据直角三角形的性质求出DF的长,利用三角形中位线定理可求出DE的长,进而可求出EF的长.
解答 解: 延长AF交BC于H,
延长AF交BC于H,
∵D为AB的中点,AF⊥BF,
∴DF=$\frac{1}{2}$AB=5,
∵D为AB的中点,E为AC的中点,
∴DE=$\frac{1}{2}$BC=8,
∴EF=DE-DF=3,
故选:B.
点评 本题考查了三角形的中位线定理和直角三角形斜边上的中线性质,中位线是三角形中的一条重要线段,由于它的性质与线段的中点及平行线紧密相连,因此,它在几何图形的计算及证明中有着广泛的应用.

练习册系列答案
相关题目
11.函数y=ax2的图象与a无关的是( )
| A. | 开口方向 | B. | 开口大小 | C. | 最高点的坐标 | D. | 对称轴 |
6.若关于x的一元二次方程x2-4x+c=0有两个相等的实数根,则常数c的值为( )
| A. | ±4 | B. | 4 | C. | ±16 | D. | 16 |
7.下列各点,不在二次函数y=x2的图象上的是( )
| A. | (1,-1) | B. | (1,1) | C. | (-2,4) | D. | (3,9) |
 二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴是x=1,有以下四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴是x=1,有以下四个结论: