题目内容
10.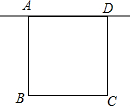 如图,在矩形ABCD中,AB=3,点P是直线AD上一点,若满足△PBC是等腰三角形的点P有且只有3个,则AD的长为3或2$\sqrt{3}$.
如图,在矩形ABCD中,AB=3,点P是直线AD上一点,若满足△PBC是等腰三角形的点P有且只有3个,则AD的长为3或2$\sqrt{3}$.
分析 要求直线AD上满足△PBC是等腰三角形的点P有且只有3个时的AB长,则需要分类讨论:①当AB=AD时;②当AB<AD时,③当AB>AD时.
解答 解:①如图,当AB=AD时
满足△PBC是等腰三角形的点P有且只有3个,
△P1BC,△P2BC是等腰直角三角形,△P3BC是等腰直角三角形(P3B=P3C),
则AB=AD=3.
②当AB<AD,且满足△PBC是等腰三角形的点P有且只有3个时,如图,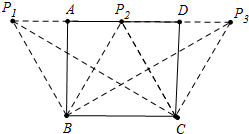
易知P2是AD的中点,BC=BP1=BP2=CP2=CP3,
此时易知△P2BC是等边三角形,
在Rt△ABP2中,∵AB=3,∠ABP2=30°,
∴AP2=AB•tan30°=$\sqrt{3}$,
∴BC=AD=2AP2=2$\sqrt{3}$
③当AB>AD时,直线AD上只有一个点P满足△PBC是等腰三角形.
故答案为:3或2 $\sqrt{3}$.
点评 本题考查矩形的性质,等腰三角形的性质等知识,解题的关键是理解题意,属于中考常考题型.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
5.在平面直角坐标系中,若直线y=ax-b经过第一、二、三象限,则直线y=bx-a不经过的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.下列事件中,必然事件是( )
| A. | 6月14日晚上能看到月亮 | |
| B. | 早晨的太阳从东方升起 | |
| C. | 打开初三数学书本,正好翻到第21页 | |
| D. | 任意掷一枚均匀的硬币,正面朝上 |
 如图,某中学制作了学生拓展性课程中选择棋类、球类、美术、书法四门课程情况的扇形统计图,从图中可以看出选择书法的学生的百分比为10%.
如图,某中学制作了学生拓展性课程中选择棋类、球类、美术、书法四门课程情况的扇形统计图,从图中可以看出选择书法的学生的百分比为10%. 把如图所示的图形折成一个正方体的盒子,折好后与“顺”相对的字是考.
把如图所示的图形折成一个正方体的盒子,折好后与“顺”相对的字是考.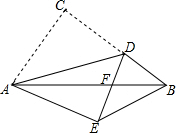 如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点E处,连接DE交AB于点F,当△DEB是直角三角形时,DF的长为$\frac{3}{2}$或$\frac{3}{4}$.
如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点E处,连接DE交AB于点F,当△DEB是直角三角形时,DF的长为$\frac{3}{2}$或$\frac{3}{4}$.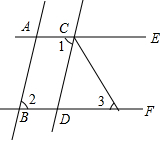 如图,已知AB∥CD,∠1=∠2,CF平分∠DCE.
如图,已知AB∥CD,∠1=∠2,CF平分∠DCE.