题目内容
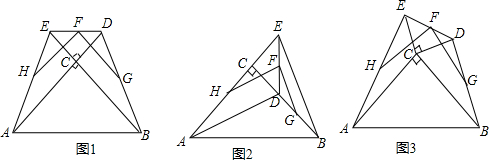
9. 如图,A在DE上,F在AB上,且AC=CE,∠1=∠2=∠3,则DE的长等于( )
如图,A在DE上,F在AB上,且AC=CE,∠1=∠2=∠3,则DE的长等于( )| A. | DC | B. | BC | C. | AB | D. | AE+AC |
分析 通过角的计算可得出∠B=∠D、∠BCA=∠DCE,再结合AC=CE即可证出△ABC≌△EDC(AAS),由此即可得出DE=BA,此题得解.
解答 解:∵∠1=∠2,∠AFD=∠CFB,∠1+∠AFD+∠D=180°=∠2+∠CFB+∠B,
∴∠B=∠D.
∵∠2=∠3,∠DCE=∠DCA+∠3,∠BCA=∠2+∠DCA,
∴∠BCA=∠DCE.
在△ABC和△EDC中,$\left\{\begin{array}{l}{∠B=∠D}\\{∠BCA=∠DCE}\\{AC=EC}\end{array}\right.$,
∴△ABC≌△EDC(AAS),
∴DE=BA.
故选C.
点评 本题考查了全等三角形的判定与性质、对顶角以及三角形内角和定理,通过角的计算求出∠B=∠D、∠BCA=∠DCE是解题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
1. 选项中展开后与如图所示的图形相同的是( )
选项中展开后与如图所示的图形相同的是( )
 选项中展开后与如图所示的图形相同的是( )
选项中展开后与如图所示的图形相同的是( )| A. |  | B. |  | C. |  | D. |  |
18.下列分数中不能化成有限小数的是( )
| A. | $\frac{9}{16}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{18}$ | D. | $\frac{7}{50}$ |