题目内容
10. 如图,菱形ABCD的周长是8cm,AB的长是2cm.
如图,菱形ABCD的周长是8cm,AB的长是2cm.
分析 根据菱形的四边相等即可解决问题.
解答 解:∵四边形ABCD是菱形,
∴AB=BC=CD=DA,
∵AB+BC+CD+DA=8cm,
∴AB=2cm,
∴AB的长为2cm.
故答案为2.
点评 本题考查菱形的性质,记住菱形的四边相等是解决问题的关键,属于基础题,中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.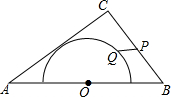 如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是( )
如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是( )
 如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是( )
如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是( )| A. | 6 | B. | 2$\sqrt{13}$+1 | C. | 9 | D. | $\frac{32}{2}$ |
1.计算2a2+a2,结果正确的是( )
| A. | 2a4 | B. | 2a2 | C. | 3a4 | D. | 3a2 |
5.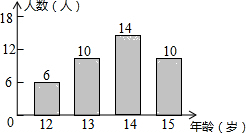 某校共有40名初中生参加足球兴趣小组,他们的年龄统计情况如图所示,则这40名学生年龄的中位数是( )
某校共有40名初中生参加足球兴趣小组,他们的年龄统计情况如图所示,则这40名学生年龄的中位数是( )
 某校共有40名初中生参加足球兴趣小组,他们的年龄统计情况如图所示,则这40名学生年龄的中位数是( )
某校共有40名初中生参加足球兴趣小组,他们的年龄统计情况如图所示,则这40名学生年龄的中位数是( )| A. | 12岁 | B. | 13岁 | C. | 14岁 | D. | 15岁 |
2.一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )
| A. | 108° | B. | 90° | C. | 72° | D. | 60° |
19.在一个布口袋里装有白、红、黑三种颜色的小球,它们除颜色外没有任何区别,其中白球2只,红球6只,黑球4只,将袋中的球搅匀,闭上眼睛随机从袋中取出1只球,则取出黑球的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
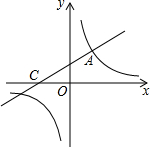 如图,直线y=$\frac{1}{2}$x+2与双曲线相交于点A(m,3),与x轴交于点C.
如图,直线y=$\frac{1}{2}$x+2与双曲线相交于点A(m,3),与x轴交于点C. 在△ABC中,BD⊥AC于D,FG⊥AC于G,DE∥BC,说出∠1和∠2的大小关系,并说明理由.
在△ABC中,BD⊥AC于D,FG⊥AC于G,DE∥BC,说出∠1和∠2的大小关系,并说明理由.