题目内容
如图1,在平面直角坐标系中,点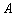 的坐标为(—4,4),点
的坐标为(—4,4),点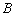 的坐标为(0,2).
的坐标为(0,2).
(1)求直线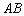 的解析式;
的解析式;
(2)以点A为直角顶点作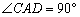 ,射线
,射线 交
交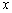 轴的负半轴于点
轴的负半轴于点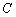 ,射线
,射线 交
交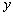 轴的负半轴于点
轴的负半轴于点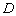 .当
.当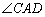 绕着点
绕着点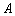 旋转时,
旋转时, 的值是否发生变化,若不变,求出它的值;若变化,求出它的变化范围;
的值是否发生变化,若不变,求出它的值;若变化,求出它的变化范围;
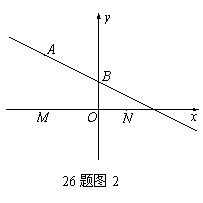
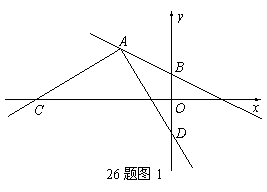 (3)如图2,点
(3)如图2,点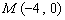 和
和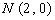 是x轴上的两个点,点
是x轴上的两个点,点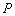 是直线
是直线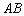 上一点.当
上一点.当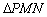 是直角三角形时,请求出满足条件的所有点
是直角三角形时,请求出满足条件的所有点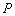 的坐标.
的坐标.
解:(1)设直线AB的解析式为: .
.
∵点 ,点
,点 在直线AB上,
在直线AB上,
∴
解得 
∴直线 的解析式为:
的解析式为: .
.
(2)不变.理由如下:
过点 分别作
分别作 轴,
轴, 轴的垂线,垂足分别为
轴的垂线,垂足分别为 ,
, (如答图).
(如答图).
 则
则 .
.
 又∵
又∵ ,
,
∴ ,即
,即 .
.
∵ ,即
,即
∴ .
.
∵ ,
,
∴ =4.
=4.
又∵ ,
, ,
,
∴ ≌
≌ .
.
∴ .
.
∴
 =8.
=8.
故 的值不发生变化,值为8
的值不发生变化,值为8
(3)①当M为直角顶点时,点P的横坐标为-4.
∵点P在直线AB上,
将 代入
代入 得,
得, .
.
∴点P的坐标为 .
.
②当N为直角顶点时,点P的横坐标为2.
∵点P在直线AB上,
将 代入
代入 得,
得, .
.
∴点P的坐标为
③当P为直角顶点时,
∵点 在直线AB上,可设点P的坐标为(
在直线AB上,可设点P的坐标为( ,
, ),
),
则 ,
, ,
,
在Rt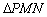 中,
中, ,MN=6,
,MN=6,
∴ .
.
解得  ,
, .
.
∴ 或
或 .
.
综上所述,满足条件的所有点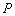 的坐标为
的坐标为 或
或 或
或 或
或 .
.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
小青在八年级上学期各次数学考试的成绩如下表:
| 考试类别 | 平时 | 期中考试 | 期末考试 | |||
| 测验1 | 测验2 | 测验3 | 测验4 | |||
| 成绩(分) | 132 | 105 | 146 | 129 | 134 | 130 |
 (1)求小青该学期平时测验的平均成绩;
(1)求小青该学期平时测验的平均成绩;
(2)如果学期的总评成绩是根据右图所示的权重计算,
请计算出小青该学期的总评成绩.
 ,则tan
,则tan = .
= . 的最大真分数是( ),最小假分数是( ),把这个假分数再添上( )个这样的分数单位就是最小的素数.
的最大真分数是( ),最小假分数是( ),把这个假分数再添上( )个这样的分数单位就是最小的素数. 并写出该不等式组的整数解.
并写出该不等式组的整数解.