题目内容
15. 如图:△ABC中,∠A=40°,∠B=60°,CD⊥AB于D,CE平分∠ACB,DF⊥CE于F,则∠CDF=80°.
如图:△ABC中,∠A=40°,∠B=60°,CD⊥AB于D,CE平分∠ACB,DF⊥CE于F,则∠CDF=80°.
分析 首先根据三角形的内角和定理求得∠ACB的度数,以及∠BCD的度数,根据角平分线的定义求得∠BCE的度数,则∠ECD可以求解,然后在△CDF中,利用内角和定理即可求得∠CDF的度数.
解答 解:∵∠A=40°,∠B=60°,
∴∠ACB=180°-∠A-∠B=80°.
∵CE平分∠ACB,
∴∠ACE=$\frac{1}{2}$∠ACB=40°.
∵CD⊥AB于D,
∴∠CDA=90°,
∠ACD=180°-∠A-∠CDA=50°.
∴∠ECD=∠ACD-∠ACE=10°.
∵DF⊥CE,
∴∠CFD=90°,
∴∠CDF=180°-∠CFD-∠DCF=80°.
故答案为:80°.
点评 本题考查了三角形的内角和等于180°以及角平分线的定义,是基础题,准确识别图形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.二元一次方程2x+y=4的自然数解有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.下列多项式中,能够因式分解的是( )
| A. | a2+b2 | B. | p2-6p+9 | C. | x2-xy+y2 | D. | -m2-n2 |
7. 如图,△ABC中,BC边上的高是( )
如图,△ABC中,BC边上的高是( )
 如图,△ABC中,BC边上的高是( )
如图,△ABC中,BC边上的高是( )| A. | AD | B. | BE | C. | CF | D. | BF |
 如图:在△ABC中,∠BAC=60°,∠1=∠2,∠3=∠4,求∠DAC的度数?
如图:在△ABC中,∠BAC=60°,∠1=∠2,∠3=∠4,求∠DAC的度数?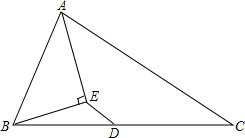 如图,△ABC中,D是BC边的中点,AE平分∠BAC,BE⊥AE于E,若AB=5,AC=7,求ED.
如图,△ABC中,D是BC边的中点,AE平分∠BAC,BE⊥AE于E,若AB=5,AC=7,求ED.