题目内容
 如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点.
如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点.(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.
考点:待定系数法求二次函数解析式,一次函数的图象,抛物线与x轴的交点,二次函数与不等式(组)
专题:代数综合题
分析:(1)根据二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点,代入得出关于a,b,c的三元一次方程组,求得a,b,c,从而得出二次函数的解析式;
(2)令y=0,解一元二次方程,求得x的值,从而得出与x轴的另一个交点坐标;
(3)画出图象,再根据图象直接得出答案.
(2)令y=0,解一元二次方程,求得x的值,从而得出与x轴的另一个交点坐标;
(3)画出图象,再根据图象直接得出答案.
解答: 解:(1)∵二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点,
解:(1)∵二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点,
∴
,
∴a=
,b=-
,c=-1,
∴二次函数的解析式为y=
x2-
x-1;
(2)当y=0时,得
x2-
x-1=0;
解得x1=2,x2=-1,
∴点D坐标为(-1,0);
(3)图象如图,
当一次函数的值大于二次函数的值时,x的取值范围是-1<x<4.
 解:(1)∵二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点,
解:(1)∵二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点,∴
|
∴a=
| 1 |
| 2 |
| 1 |
| 2 |
∴二次函数的解析式为y=
| 1 |
| 2 |
| 1 |
| 2 |
(2)当y=0时,得
| 1 |
| 2 |
| 1 |
| 2 |
解得x1=2,x2=-1,
∴点D坐标为(-1,0);
(3)图象如图,
当一次函数的值大于二次函数的值时,x的取值范围是-1<x<4.
点评:本题考查了用待定系数法求二次函数的解析式以及一次函数的图象、抛物线与x轴的交点问题,是中档题,要熟练掌握.

练习册系列答案
相关题目
下列命题:
①对顶角相等;
②等腰三角形的两个底角相等;
③两直线平行,同位角相等.
其中逆命题为真命题的有( )
①对顶角相等;
②等腰三角形的两个底角相等;
③两直线平行,同位角相等.
其中逆命题为真命题的有( )
| A、①② | B、②③ | C、①③ | D、①②③ |
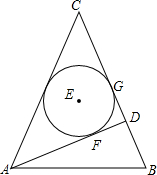 如图,在等腰△ABC中,CA=CB,AD是腰BC边上的高,△ACD的内切圆⊙E分别与边AD、BC相切于点F、G,连AE、BE.
如图,在等腰△ABC中,CA=CB,AD是腰BC边上的高,△ACD的内切圆⊙E分别与边AD、BC相切于点F、G,连AE、BE.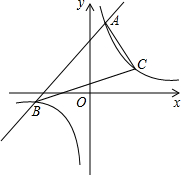 已知一次函数y1=x+m的图象与反比例函数
已知一次函数y1=x+m的图象与反比例函数 如图,点A、B分别在x,y轴上,点D在第一象限内,DC⊥x轴于点C,AO=CD=2,AB=DA=
如图,点A、B分别在x,y轴上,点D在第一象限内,DC⊥x轴于点C,AO=CD=2,AB=DA=