题目内容
如图，ABCD是⊙O的内接四边形，AB是⊙O的直径，过点D的切线交BA的延长线于点E，若∠ADE=25°，则∠C= 度．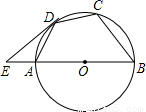
【答案】分析：连接OD，根据切线的性质定理，得OD⊥DE，从而求得∠ADO的度数，根据等边对等角得到∠OAD=∠ADO；再根据圆内接四边形的对角互补，即可求得∠C的度数．
解答：
解：连接OD，
∵过点D的切线交BA的延长线于点E，
∴OD⊥DE，
∴∠ADO=90°-∠ADE=65°；
∵OA=OD，
∴∠OAD=∠ADO=65°，
∴∠C=115°．
点评：此题综合运用了切线的性质定理，圆内接四边形的性质．
解答：
解：连接OD，∵过点D的切线交BA的延长线于点E，
∴OD⊥DE，
∴∠ADO=90°-∠ADE=65°；
∵OA=OD，
∴∠OAD=∠ADO=65°，
∴∠C=115°．
点评：此题综合运用了切线的性质定理，圆内接四边形的性质．
练习册系列答案
相关题目
如图四边形ABCD是⊙O的内接四边形，AB是⊙O的直径，若再增加一个条件，就可使四边形ABCD成为等腰梯形，你所增加的条件是（只写出一个条件，图中不再增加其他的字母和线段．（给出证明）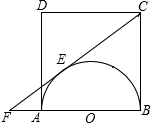
如图，ABCD是边长为2 a的正方形，AB为半圆O的直径，CE切⊙O于E，与BA的延长线交于F，求EF的长．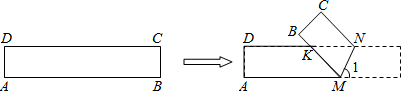
如图，ABCD是边长为1的正方形，EFGH是内接于ABCD的正方形，AE=a，AF=b，若SEFGH=| 2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，ABCD是正方形，G是BC上的一点，DE⊥AG于E，BF⊥AG于F．