题目内容
7.为保护环境,发展低碳经济,某单位在科研部门的支持下,进行了技术攻关,采用了新工艺把二氧化碳转化为一种可利用的化工产品,已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本y(元)与月处理量x(吨)之间的函数关系可近似地表示为:y=$\frac{1}{2}$x2-200x+80000,且每处理1吨二氧化碳得到可利用的化工产品价值为100元,设该单位每月获利为S元,则该单位每月能否盈利?如果盈利,求出最大利润;如果不盈利,则国家至少需要补贴多少元才能使该单位不亏损?分析 根据题意得出S=100x-y,进而代入利用配方法求出二次函数最值即可.
解答 解:由题意可得:该单位每月获利为S=100x-y,
则S=100x-($\frac{1}{2}$x2-200x+80000)
=-$\frac{1}{2}$x2+330x-80000,
=-$\frac{1}{2}$(x-300)2-35000,
∵400≤x≤600,
∴当x=400时,S有最大值为:-40000,
∴该单位不获利,需要国家每月至少补贴40000元,才能不亏损.
点评 此题主要考查二次函数的应用,根据题意得出S与x的函数关系式是解题关键.

练习册系列答案
相关题目
18.某工厂计划生产A、B两种产品共10件,其生产成本和利润如下表.
(1)若工厂生产成本不多于35万元,且获利多于15万元,问工厂有哪几种生产方案?
(2)在(1)的条件下,哪种生产方案获利最大?并求出最大利润.
| A种产品 | B种产品 | |
| 成本(万元/件) | 2 | 5 |
| 利润(万元/件) | 1 | 3 |
(2)在(1)的条件下,哪种生产方案获利最大?并求出最大利润.
19.近期由于雾霾严重,不少市民选择佩戴口罩出行,某药店购进甲种可预防PM2.5的N95型口罩和乙种普通口罩共400个,这两种口罩的进价和售价如表所示:
该药店计划购进乙种口罩x个,两种口罩全部销售完后可获毛利润y元.
注:毛利润=(售价-进价)×销售量
(1)求出毛利润y与x的函数关系式;
(2)已知甲种口罩的数量不多于乙种口罩数量的3倍,该药店怎样进货,使全部销售获得的毛利润最大?并求出最大毛利润.
| 甲 | 乙 | |
| 进价(元/个) | 18 | 6 |
| 售价(元/个) | 22 | 9 |
注:毛利润=(售价-进价)×销售量
(1)求出毛利润y与x的函数关系式;
(2)已知甲种口罩的数量不多于乙种口罩数量的3倍,该药店怎样进货,使全部销售获得的毛利润最大?并求出最大毛利润.
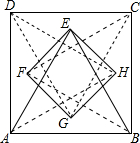 如图,分别以正方形ABCD的四条边为边,向其内部作等边三角形,得到△ABE、△BCF、△CDG、△DAH,连接EF、FG、GH、HE,若AB=2,则四边形EFGH的面积为8-4$\sqrt{3}$.
如图,分别以正方形ABCD的四条边为边,向其内部作等边三角形,得到△ABE、△BCF、△CDG、△DAH,连接EF、FG、GH、HE,若AB=2,则四边形EFGH的面积为8-4$\sqrt{3}$. 如图,在△ABC中,M、E把AC边三等分,MN∥EF∥BC,MN、EF把△ABC分成三部分,则自上而下三部分的面积比为1:3:5.
如图,在△ABC中,M、E把AC边三等分,MN∥EF∥BC,MN、EF把△ABC分成三部分,则自上而下三部分的面积比为1:3:5. 如图,在矩形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C→D作匀速运动,那么△ABP的面积y与点P运动的路程x之间的函数图象大致是( )
如图,在矩形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C→D作匀速运动,那么△ABP的面积y与点P运动的路程x之间的函数图象大致是( )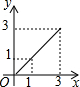



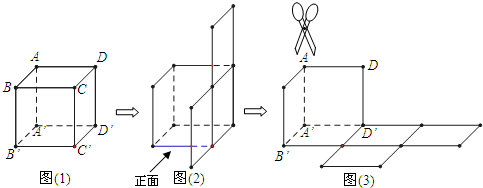
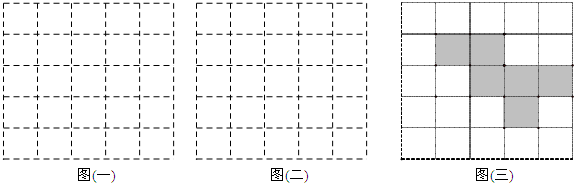
 ).
).