题目内容
16.已知正方形ABCD的对角线AC,BD相交于点O.(1)如图1,E,G分别是OB,OC上的点,CE与DG的延长线相交于点F.若DF⊥CE,求证:OE=OG;
(2)如图2,H是BC上的点,过点H作EH⊥BC,交线段OB于点E,连结DH交CE于点F,交OC于点G.若OE=OG,
①求证:∠ODG=∠OCE;
②当AB=1时,求HC的长.
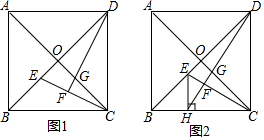
分析 (1)欲证明OE=OG,只要证明△DOG≌△COE(ASA)即可;
(2)①欲证明∠ODG=∠OCE,只要证明△ODG≌△OCE即可;
②设CH=x,由△CHE∽△DCH,可得$\frac{EH}{HC}$=$\frac{HC}{CD}$,即HC2=EH•CD,由此构建方程即可解决问题;
解答 (1)证明:如图1中,∵四边形ABCD是正方形,
∴AC⊥BD,OD=OC,
∴∠DOG=∠COE=90°,
∴∠OEC+∠OCE=90°,
∵DF⊥CE,
∴∠OEC+∠ODG=90°,
∴∠ODG=∠OCE,
∴△DOG≌△COE(ASA),
∴OE=OG.
(2)①证明:如图2中,∵OG=OE,∠DOG=∠COE=90°OD=OC,
∴△ODG≌△OCE,
∴∠ODG=∠OCE.
②解:设CH=x,
∵四边形ABCD是正方形,AB=1,
∴BH=1-x,∠DBC=∠BDC=∠ACB=45°,
∵EH⊥BC,
∴∠BEH=∠EBH=45°,
∴EH=BH=1-x,
∵∠ODG=∠OCE,
∴∠BDC-∠ODG=∠ACB-∠OCE,
∴∠HDC=∠ECH,
∵EH⊥BC,
∴∠EHC=∠HCD=90°,
∴△CHE∽△DCH,
∴$\frac{EH}{HC}$=$\frac{HC}{CD}$,
∴HC2=EH•CD,
∴x2=(1-x)•1,
解得x=$\frac{\sqrt{5}-1}{2}$或$\frac{-\sqrt{5}-1}{2}$(舍弃),
∴HC=$\frac{\sqrt{5}-1}{2}$.
点评 本题考查正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
6.H7N9禽流感病毒的直径大约为0.0000000805米,这个数用科学记数法表示为( )
| A. | 8.05×10-8 | B. | 8.05×10-7 | C. | 80.5×10-9 | D. | 0.805×10-7 |
4. 如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则( )
如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则( )
 如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则( )
如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD=x,tan∠ACB=y,则( )| A. | x-y2=3 | B. | 2x-y2=9 | C. | 3x-y2=15 | D. | 4x-y2=21 |
8.下列运算中,正确的是( )
| A. | 7a+a=7a2 | B. | a2•a3=a6 | C. | a3÷a=a2 | D. | (ab)2=ab2 |
5.若a-b=2,b-c=-3,则a-c等于( )
| A. | 1 | B. | -1 | C. | 5 | D. | -5 |
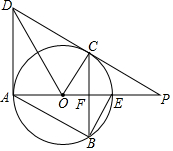 如图所示,直线DP和圆O相切于点C,交直径AE的延长线于点P.过点C作AE的垂线,交AE于点F,交圆O于点B.作平行四边形ABCD,连接BE,DO,CO.
如图所示,直线DP和圆O相切于点C,交直径AE的延长线于点P.过点C作AE的垂线,交AE于点F,交圆O于点B.作平行四边形ABCD,连接BE,DO,CO.