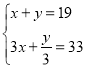Question

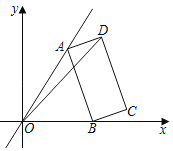
【题目】如图，矩形ABCD的两个顶点A、B分别在x、y轴上，顶点C、D位于第二象限，且OA=3，OB=2，对角线AC、BD交于点G，若双曲线经过C、G，则k=__________．

Answer 1

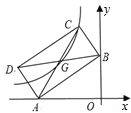
【答案】-3.5

【解析】

分别过C、G两点作x轴的垂线，交x轴于点E、F，作CH⊥y轴于H，设，根据矩形的性质与平行线分线段成比例得出点G的坐标，根据反比例函数系数k＝xy求出点m，通过证明△AOB∽△BHC，求得CE，得出点C坐标，进而求解．

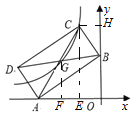
如图，分别过C、G两点作x轴的垂线，交x轴于点E、F，作CH⊥y轴于H，

∴CE∥GF，设，

∵四边形ABCD是矩形，

∴AG＝CG，

∴GF＝CE，EF＝，

∴OF＝，

∴，

∵曲线经过点C、G，

∴，

解得，，

∴CH＝1，

∵∠ABC＝90°，

∴∠CBH+∠ABO＝90°，

∵∠OAB+∠ABO＝90°，

∴∠OAB＝∠CBH，

∵∠AOB＝∠BHC＝90°，

∴△AOB∽△BHC，

∴，即，

∴BH＝，

∴OH＝，

∴，

∴，

故答案为：-3.5．