题目内容
12.已知方程x2+3x+m=0的一个根比另一个根大2,则m=$\frac{5}{4}$.分析 设方程的一个根为t,则另一个根为t+2,根据根与系数的关系得到t+t+2=-3,t(t+2)=m,然后先求出t的值再计算m的值.
解答 解:设方程的一个根为t,则另一个根为t+2,
根据题意得t+t+2=-3,t(t+2)=m,
所以t=-$\frac{5}{2}$,
所以m=-$\frac{5}{2}$×(-$\frac{5}{2}$+2)=$\frac{5}{4}$.
故答案为$\frac{5}{4}$.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
相关题目
7.某商场试销一种商品,成本为每件200元,规定试销期间销售单价不低于成本单价,且获利不得高于50%,一段时间后,发现销售量y(件)与销售单价x(元)之间的函数关系如表:
(1)请根据表格中所给数据,求出y关于x的函数关系式;
(2)设商场所获利润为w元,将商品销售单价定为多少时,才能使所获利润最大?最大利润是多少?
| 销售单价x(元) | … | 230 | 235 | 240 | 245 | … |
| 销售量y(件) | … | 440 | 430 | 420 | 410 | … |
(2)设商场所获利润为w元,将商品销售单价定为多少时,才能使所获利润最大?最大利润是多少?
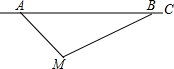 根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速40千米/时,已知交警测速点M到该公路A点的距离为10$\sqrt{2}$米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.
根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速40千米/时,已知交警测速点M到该公路A点的距离为10$\sqrt{2}$米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.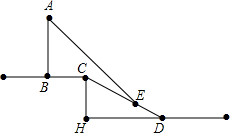 如图,小明测得树AB落在水平地面上的影长BC为 2.4 米,落在坡面上的影长CE为3.2米,身高是1.6米的小明站在坡面上,影子也都落在坡面上,长度为2米.已知坡面的铅直高度CH与水平距离DH的比为3:4,试求树AB的高度.
如图,小明测得树AB落在水平地面上的影长BC为 2.4 米,落在坡面上的影长CE为3.2米,身高是1.6米的小明站在坡面上,影子也都落在坡面上,长度为2米.已知坡面的铅直高度CH与水平距离DH的比为3:4,试求树AB的高度.