题目内容
7.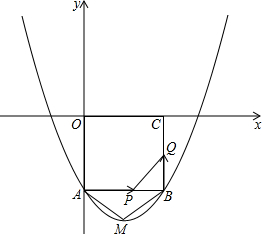 如图,在平面直角坐标系xOy中,正方形OABC的边长为2cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B,最低点为M,且S△AMB=$\frac{5}{6}$
如图,在平面直角坐标系xOy中,正方形OABC的边长为2cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B,最低点为M,且S△AMB=$\frac{5}{6}$(1)求此抛物线的解析式,并说明这条抛物线是由抛物线y=ax2 怎样平移得到的;
(2)如果点P由点A开始沿着射线AB以2cm/s的速度移动,同时点Q由点B开始沿BC边以1cm/s的速度向点C移动,当其中一点到达终点时运动结束;
①在运动过程中,P、Q两点间的距离是否存在最小值?如果存在,请求出它的最小值;
②当PQ取得最小值时,在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是梯形?如果存在,求出R点的坐标;如果不存在,请说明理由.
分析 (1)过M作MN⊥x轴于N,交AB于Q,求出A、B、M的坐标,代入即可求出解析式,化成顶点式,即可得出答案;
(2)①根据勾股定理求出PQ2=(2-2t)2+t2=5(t-$\frac{4}{5}$)2+$\frac{4}{5}$,即可得出答案;②分为两种情况:第一种情况:当AB∥QR时,
由①知:t=$\frac{4}{5}$,求出BQ=$\frac{4}{5}$,CQ=2-$\frac{4}{5}$=$\frac{6}{5}$,把y=-$\frac{6}{5}$代入抛物线的解析式求出即可;第二种情况:当BR∥PQ时,求出即可.
解答 解:(1)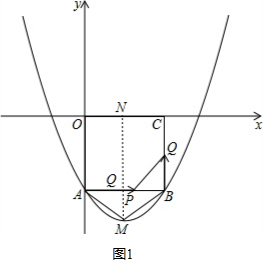
过M作MN⊥x轴于N,交AB于Q,如图1,
∵正方形OABC的边长为2cm,
∴OA=AB=BC=OC=2cm,
∴A(0,-2),B(2,-2),AQ=BQ=1cm,
∵S△AMB=$\frac{5}{6}$,
∴$\frac{1}{2}$×2×MQ=$\frac{5}{6}$,
MQ=$\frac{5}{6}$,
即M的坐标为(1,$\frac{17}{6}$),
把A、B、M的坐标代入y=ax2+bx+c得:$\left\{\begin{array}{l}{c=-2}\\{4a+2b+c=-2}\\{a+b+c=\frac{17}{6}}\end{array}\right.$
解得:a=$\frac{5}{6}$,b=-$\frac{5}{3}$,c=-2,
即此抛物线的解析式是y=$\frac{5}{6}$x2-$\frac{5}{3}$x-2,
即y=$\frac{5}{6}$(x-1)2-$\frac{17}{6}$,
所以这条抛物线是由抛物线y=ax2 向右1个单位长度,向下$\frac{17}{6}$个单位长度得到的;
(2)①PQ2=(2-2t)2+t2=5(t-$\frac{4}{5}$)2+$\frac{4}{5}$,
当t=$\frac{4}{5}$时,最小值$\frac{{2\sqrt{5}}}{5}$,
即在运动过程中,P、Q两点间的距离存在最小值,它的最小值是$\frac{2\sqrt{5}}{5}$,
②分为两种情况:如图2,第一种情况:当AB∥QR时,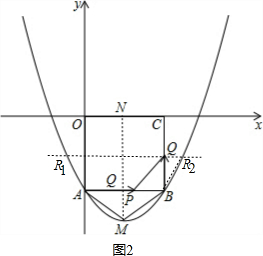
由①知:t=$\frac{4}{5}$,BQ=$\frac{4}{5}$,CQ=2-$\frac{4}{5}$=$\frac{6}{5}$,
所以把y=-$\frac{6}{5}$代入抛物线的解析式得:$\frac{5}{6}$(x-1)2-$\frac{17}{6}$=-$\frac{6}{5}$,
解得:x1=$-\frac{2}{5}$,x2=$\frac{12}{5}$
当x1=$-\frac{2}{5}$时,说明P、B、Q、R为顶点的四边形是梯形,
当x2=$\frac{12}{5}$时,PBRQ为平行四边形,舍去,
第二种情况:当BR∥PQ时,与x2=$\frac{12}{5}$的情况相同,故此时不存在梯形,
∴R($\frac{12}{5}$,-$\frac{6}{5}$).
点评 本题考查了二次函数的最值,用待定系数法求二次函数的解析式,梯形的性质,平行四边形的性质的应用,能综合运用知识点进行计算是解此题的关键,用了分类讨论思想,难度偏大.

 期末冲刺100分创新金卷完全试卷系列答案
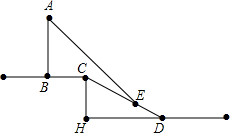
期末冲刺100分创新金卷完全试卷系列答案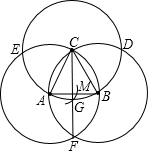 如图,分别以边长1为的等边三角形ABC的顶点为圆心,以其边长为半径作三个等圆,得交点D、E、F,连接CF交⊙C于点G,以点E为圆心,EG长为半径画弧,交边AB于点M,求AM的长.
如图,分别以边长1为的等边三角形ABC的顶点为圆心,以其边长为半径作三个等圆,得交点D、E、F,连接CF交⊙C于点G,以点E为圆心,EG长为半径画弧,交边AB于点M,求AM的长.
 如图,小明测得树AB落在水平地面上的影长BC为 2.4 米,落在坡面上的影长CE为3.2米,身高是1.6米的小明站在坡面上,影子也都落在坡面上,长度为2米.已知坡面的铅直高度CH与水平距离DH的比为3:4,试求树AB的高度.
如图,小明测得树AB落在水平地面上的影长BC为 2.4 米,落在坡面上的影长CE为3.2米,身高是1.6米的小明站在坡面上,影子也都落在坡面上,长度为2米.已知坡面的铅直高度CH与水平距离DH的比为3:4,试求树AB的高度.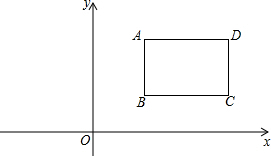 在平面直角坐标系和第一象限中有一矩形ABCD,AD平行于x轴,其中点A(3,4)且AB=2,BC=3.若将矩形ABCD向左平移a个单位之后,矩形到了第二象限,这时B、D两点在同一双曲线y=$\frac{k}{x}$上.
在平面直角坐标系和第一象限中有一矩形ABCD,AD平行于x轴,其中点A(3,4)且AB=2,BC=3.若将矩形ABCD向左平移a个单位之后,矩形到了第二象限,这时B、D两点在同一双曲线y=$\frac{k}{x}$上.