题目内容
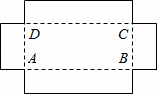
如图,用一块长为50cm、宽为30cm的长方形铁片制作一个无盖的盒子,若在铁片的四个角截去四个相同的小正方形,设小正方形的边长为xcm.
(1)底面的长AB=cm,宽BC=cm(用含x的代数式表示)
(2)当做成盒子的底面积为300cm2时,求该盒子的容积.
(3)该盒子的侧面积S是否存在最大的情况?若存在,求出x的值及最大值是多少?若不存在,说明理由.
 .
.
解:(1)∵用一块长为50cm、宽为30cm的长方形铁片制作一个无盖的盒子,在铁片的四个角截去四个相同的小正方形,
设小正方形的边长为xcm,
∴底面的长AB=(50﹣2x)c m,宽BC=(30﹣2x)cm,
m,宽BC=(30﹣2x)cm,
故答案为:50﹣2x,30﹣2x;
(2)依题意,得:
(50﹣2x)(30﹣2x)=300
整理,得:x2﹣40x+300=0
解得:x1=10,x2=30(不符合题意,舍去)
当x1=10时,盒子容积=(50﹣20)(30﹣20)×10=3000(cm3);
(3)盒子的侧面积为:
S=2x(50﹣2x)+2x(30﹣2x)
=100x﹣4x2+60x﹣4x2
=﹣8x2+160x=﹣8(x2﹣20x)
=﹣8[(x﹣10)2﹣100]
=﹣8(x﹣10)2+800
∵﹣8(x﹣10)2≤0,
∴﹣8(x﹣10)2+800≤800,
∴当x=10时,S有最大值,最大值为800.

某县为发展教育事业,加强了对教育经费的投入,已知2009年投入教育经费5000万元,预计2011年投入教育经费8000万元.设投入教育经费的年平均增长率为x,根据题意,列方程(只要求列方程,不要求解)
某合作学习小组的6名同学在一次数学测试中,成绩分布为76,88,96,82,78,96,这组数据的中位数是( )
|
| A. | 82 | B. | 85 | C. | 88 | D. | 96 |
 ÷
÷ =.
=.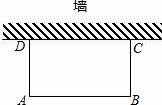
 图,某小区在宽20m,长32m的矩形地面上修筑同样宽的人行道(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,求道路的宽.
图,某小区在宽20m,长32m的矩形地面上修筑同样宽的人行道(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,求道路的宽.
 BCD是⊙O的内接四边
BCD是⊙O的内接四边 形,∠B=70°,则∠D的度数是( )
形,∠B=70°,则∠D的度数是( )
 =3,求
=3,求 的值.
的值.