题目内容
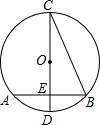 如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=4
如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=4| 2 |
考点:垂径定理,等腰直角三角形,圆周角定理
专题:
分析:连接OB,则可知∠BOD=2∠BCD=45°,由垂径定理可得BE=2
,在Rt△OEB中BE=OE,利用勾股定理可求得OB.
| 2 |
解答: 解:连接OB,
解:连接OB,
∵∠BCD=22°30′,
∴∠BOD=2∠BCD=45°,
∵CD是直径,弦AB⊥CD,
∴BE=AE=
AB=2
cm,
在Rt△BOE中,由勾股定理可求得OB=4cm,
即⊙O的半径为4cm,
故答案为:4.
 解:连接OB,
解:连接OB,∵∠BCD=22°30′,
∴∠BOD=2∠BCD=45°,
∵CD是直径,弦AB⊥CD,
∴BE=AE=
| 1 |
| 2 |
| 2 |
在Rt△BOE中,由勾股定理可求得OB=4cm,
即⊙O的半径为4cm,
故答案为:4.
点评:本题主要考查垂径定理和圆周角定理,由条件得到∠BOD=45°且求得BE的长是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 在今年第9号超强台风“圣帕”来临之际,B市气象局测得台风中心位于B市正东方向500km的A处,正以20km/h千米的速度向西北方向移动,距台风中心400的范围内受到影响,问B市是否受到这次台风的影响?如果有影响,则持续的时间有多长?
在今年第9号超强台风“圣帕”来临之际,B市气象局测得台风中心位于B市正东方向500km的A处,正以20km/h千米的速度向西北方向移动,距台风中心400的范围内受到影响,问B市是否受到这次台风的影响?如果有影响,则持续的时间有多长?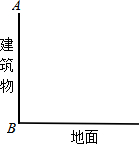 如图,为了测量某建筑物墙壁AB的高度,小明找来一根足够长的竹竿(长度大于AB)和米尺,请你设计一种测量方案,帮助小明测得AB的高度,要求:
如图,为了测量某建筑物墙壁AB的高度,小明找来一根足够长的竹竿(长度大于AB)和米尺,请你设计一种测量方案,帮助小明测得AB的高度,要求: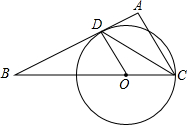 如图,在△ABC中,∠A=90°,CD平分∠ACB交AB于D,AD<AC,过C,D两点作⊙O且圆心O在BC上.若CD=5,△ADC的面积为6,求半径.
如图,在△ABC中,∠A=90°,CD平分∠ACB交AB于D,AD<AC,过C,D两点作⊙O且圆心O在BC上.若CD=5,△ADC的面积为6,求半径.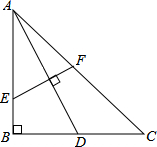 如图,已知在△ABC中,∠B=90°,AB=BC,AD是BC边上的中线,EF是AD的垂直平分线,交AB于点E,交AC于点F,求AE:BE的值.
如图,已知在△ABC中,∠B=90°,AB=BC,AD是BC边上的中线,EF是AD的垂直平分线,交AB于点E,交AC于点F,求AE:BE的值.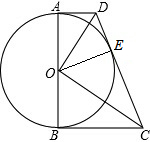 如图,AB是⊙O的直径,AD、BC、CD为⊙O的切线,设⊙O的半径为6cm,梯形ABCD的周长为42cm,
如图,AB是⊙O的直径,AD、BC、CD为⊙O的切线,设⊙O的半径为6cm,梯形ABCD的周长为42cm,