题目内容
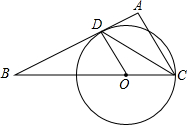如图，在△ABC中，∠A=90°，CD平分∠ACB交AB于D，AD＜AC，过C，D两点作⊙O且圆心O在BC上．若CD=5，△ADC的面积为6，求半径．考点：切线的判定与性质
专题：
分析：如图，连接DE，首先证明△ACD∽△DCE，进而得到EC=
；利用勾股定理及面积公式求出AD、AC的长度，即可解决问题．
| DC2 |
| AC |
解答：
解：如图，连接DE；
∵EC为⊙O的直径，
∴∠EDC=90°；
又∵CD平分∠ACB，
∴∠ACD=∠ECD；而∠A=90°，
∴△ACD∽△DCE，
∴
=
，
设AD=x，AC=y；
由题意得：
，
解得：x=3，y=4，
∴DC2=9+16=25，
∴EC=
，
故⊙O的半径为
．
解：如图，连接DE；∵EC为⊙O的直径，
∴∠EDC=90°；
又∵CD平分∠ACB，
∴∠ACD=∠ECD；而∠A=90°，
∴△ACD∽△DCE，
∴
| AC |
| DC |
| DC |
| EC |
设AD=x，AC=y；
由题意得：
|
解得：x=3，y=4，
∴DC2=9+16=25，
∴EC=
| 25 |
| 4 |
故⊙O的半径为
| 25 |
| 8 |
点评：该命题以圆为载体，以圆周角定理及其推论、相似三角形的判定及其性质的应用为考查的核心构造而成；解题的关键是作辅助线，构造相似三角形．
练习册系列答案
相关题目
小明在写作业时不慎将两滴墨水滴在数轴上（如图），根据图中的数据，判断墨迹盖住的正整数有如图所示，经过折叠能围成一个正方体的是（ ）
A、 |
B、 |
C、 |
D、 |
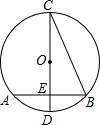如图，在⊙O中，CD是直径，弦AB⊥CD，垂足为E，连接BC，若AB=4