题目内容
 如图,BF、CE相交于A点,BE=BA,CA=CF,若D、M、N分别是BC、AE、AF的中点,试判断DM与DN是否相等.
如图,BF、CE相交于A点,BE=BA,CA=CF,若D、M、N分别是BC、AE、AF的中点,试判断DM与DN是否相等.考点:三角形中位线定理,全等三角形的判定与性质
专题:证明题
分析:DM与DN相等,过M作EB的平行线MH,过N作CF的平行线NG,连接D,DG 利用三角形的中位线定理易证DG=MH,同理DH=NG,进而可证明△MHD和≌△NGD,所以DM=DN.
解答:解:DM与DN相等,
理由如下: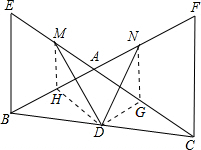
过M作EB的平行线MH交于BA于H,过N作CF的平行线NG交CA于G,连接DH,DG,
∵D、M、N分别是BC、AE、AF的中点,
∴MH=
BE,DG∥BA,
∴DG=MH,
同理:DH=NG,
在△MHD和△NGD中,
,
∴△MHD和≌△NGD(SAS),
∴DM=DN.
理由如下:

过M作EB的平行线MH交于BA于H,过N作CF的平行线NG交CA于G,连接DH,DG,
∵D、M、N分别是BC、AE、AF的中点,
∴MH=
| 1 |
| 2 |
∴DG=MH,
同理:DH=NG,
在△MHD和△NGD中,
|
∴△MHD和≌△NGD(SAS),
∴DM=DN.
点评:本题考查了三角形的中位线定理以及全等三角形的判定和性质,解题的关键是正确添加辅助线,构造全等三角形,题目的难度不小.

练习册系列答案
相关题目
下面各式中,计算正确的是( )
| A、-22=4 | |||
B、
| |||
C、
| |||
| D、(-1)3=-3 |
已知抛物线y=a(x-1)2+k与x轴交于点A(m,0),B(4,0),则A、B两点之间的距离是( )
| A、2 | B、4 | C、6 | D、8 |

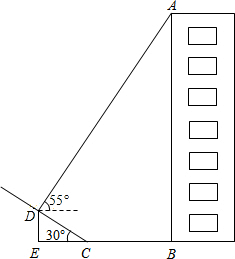 如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=4m.在D点处观察点A的仰角为55°,已知坡角为30°,你能求出楼房AB的高度吗?(sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,结果精确到0.1m)
如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=4m.在D点处观察点A的仰角为55°,已知坡角为30°,你能求出楼房AB的高度吗?(sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,结果精确到0.1m)