题目内容
20.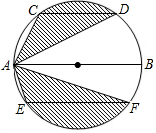 运用图形变化的方法研究下列问题:如图,AB是⊙O的直径,CD、EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8.则图中阴影部分的面积是( )
运用图形变化的方法研究下列问题:如图,AB是⊙O的直径,CD、EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8.则图中阴影部分的面积是( )| A. | $\frac{25}{2}$π | B. | 10π | C. | 24+4π | D. | 24+5π |
分析 作直径CG,连接OD、OE、OF、DG,则根据圆周角定理求得DG的长,证明DG=EF,则S扇形ODG=S扇形OEF,然后根据三角形的面积公式证明S△OCD=S△ACD,S△OEF=S△AEF,则S阴影=S扇形OCD+S扇形OEF=S扇形OCD+S扇形ODG=S半圆,即可求解.
解答 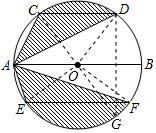 解:作直径CG,连接OD、OE、OF、DG.
解:作直径CG,连接OD、OE、OF、DG.
∵CG是圆的直径,
∴∠CDG=90°,则DG=$\sqrt{C{G}^{2}-C{D}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
又∵EF=8,
∴DG=EF,
∴$\widehat{DG}$=$\widehat{EF}$,
∴S扇形ODG=S扇形OEF,
∵AB∥CD∥EF,
∴S△OCD=S△ACD,S△OEF=S△AEF,
∴S阴影=S扇形OCD+S扇形OEF=S扇形OCD+S扇形ODG=S半圆=$\frac{1}{2}$π×52=$\frac{25}{2}$π.
故选A.
点评 本题考查扇形面积的计算,圆周角定理.本题中找出两个阴影部分面积之间的联系是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
10.实数8的立方根是( )
| A. | -2 | B. | 2 | C. | -3 | D. | 3 |
8. 一个几何体的三视图如图所示,这个几何体是( )
一个几何体的三视图如图所示,这个几何体是( )
 一个几何体的三视图如图所示,这个几何体是( )
一个几何体的三视图如图所示,这个几何体是( )| A. | 球 | B. | 圆柱 | C. | 圆锥 | D. | 立方体 |
15.下列计算正确的是( )
| A. | 2a+b=2ab | B. | (-a)2=a2 | C. | a6÷a2=a3 | D. | a3•a2=a6 |
12. 如图所示的几何体的主视图正确的是( )
如图所示的几何体的主视图正确的是( )
 如图所示的几何体的主视图正确的是( )
如图所示的几何体的主视图正确的是( )| A. |  | B. |  | C. |  | D. |  |
9.某校美术社团为练习素描,他们第一次用120元买了若干本资料,第二次用240元在同一商家买同样的资料,这次商家每本优惠4元,结果比上次多买了20本.求第一次买了多少本资料?若设第一次买了x本资料,列方程正确的是( )
| A. | $\frac{240}{x-20}$-$\frac{120}{x}$=4 | B. | $\frac{240}{x+20}$-$\frac{120}{x}$=4 | C. | $\frac{120}{x}$-$\frac{240}{x-20}$=4 | D. | $\frac{120}{x}$-$\frac{240}{x+20}$=4 |
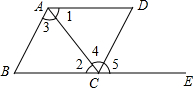 如图,下列能判定AB∥CD的条件有( )个.
如图,下列能判定AB∥CD的条件有( )个.