题目内容
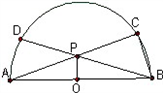
 如图,半径为1的半圆O上有两个动点A,B,若AB=1,则四边形ABCD的面积的最大值是
如图,半径为1的半圆O上有两个动点A,B,若AB=1,则四边形ABCD的面积的最大值是3
| ||
| 4 |
3
| ||
| 4 |
分析:过点O作OH⊥AB于点H,连接OA,OB,分别过点A、H、B作AE⊥CD、HF⊥CD,BG⊥CD于点E、F、G,根据垂线段线段最短可知HF<OH,再由梯形的中位线定理可知,HF=
(AE+BG),进而可得出结论.
| 1 |
| 2 |
解答: 解:过点O作OH⊥AB于点H,连接OA,OB,分别过点A、H、B作AE⊥CD、HF⊥CD,BG⊥CD于点E、F、G,
解:过点O作OH⊥AB于点H,连接OA,OB,分别过点A、H、B作AE⊥CD、HF⊥CD,BG⊥CD于点E、F、G,
∵AB=1,⊙O的半径=1,
∴OH=
,
∵垂线段最短,
∴HF<OH,
∴HF=
(AE+BG),
∴S四边形ABCD=S△AOC+S△AOB+S△BOD=
×1×AE+
×1×
+
×1×BG
=
AE+
+
BG
=
(AE+BG)+
=HF+
≤OH+
=
+
=
.
故答案为:
.
 解:过点O作OH⊥AB于点H,连接OA,OB,分别过点A、H、B作AE⊥CD、HF⊥CD,BG⊥CD于点E、F、G,
解:过点O作OH⊥AB于点H,连接OA,OB,分别过点A、H、B作AE⊥CD、HF⊥CD,BG⊥CD于点E、F、G,∵AB=1,⊙O的半径=1,
∴OH=
| ||
| 2 |
∵垂线段最短,
∴HF<OH,
∴HF=
| 1 |
| 2 |
∴S四边形ABCD=S△AOC+S△AOB+S△BOD=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| ||
| 4 |
=HF+
| ||
| 4 |
| ||
| 4 |
| ||
| 2 |
| ||
| 4 |
3
| ||
| 4 |
故答案为:
3
| ||
| 4 |
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出等边三角形是解答此题的关键.

练习册系列答案
相关题目
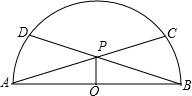 如图,半径为2的半圆O中有两条相等的弦AC与BD相交于点P.
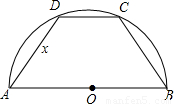
如图,半径为2的半圆O中有两条相等的弦AC与BD相交于点P.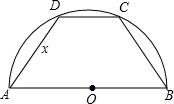 如图,半径为1的半圆内接等腰梯形,其下底是半圆的直径,试求:
如图,半径为1的半圆内接等腰梯形,其下底是半圆的直径,试求: