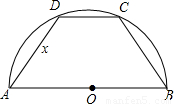
题目内容
如图，半径为2的半圆O中有两条相等的弦AC与BD相交于点P．
（1）求证：PO⊥AB；
（2）若BC=1，则PO的长是 _________ ．
（1）求证：PO⊥AB；
（2）若BC=1，则PO的长是 _________ ．
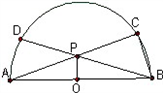
（1）证明：连接AD．
∵AB是直径
∴∠ACB=∠ADB=90°
∵AC=BD，AB=BA
∴△ABC≌△ABD
∴∠BAC=∠ABD
从而PA=PB．
∵⊙O是AB中点，
∴PO⊥AB
（2）解：∵∠AOP=∠ACB=90°，∠OAP=∠CAB
∴△AOP∽△ACB
∴
∵AB=4，BC=1
∴AC=
=
∴OP=
=
．
∵AB是直径
∴∠ACB=∠ADB=90°
∵AC=BD，AB=BA
∴△ABC≌△ABD
∴∠BAC=∠ABD
从而PA=PB．
∵⊙O是AB中点，
∴PO⊥AB
（2）解：∵∠AOP=∠ACB=90°，∠OAP=∠CAB
∴△AOP∽△ACB
∴
∵AB=4，BC=1
∴AC=
=∴OP=
=． 
练习册系列答案
相关题目
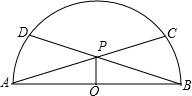如图，半径为2的半圆O中有两条相等的弦AC与BD相交于点P．
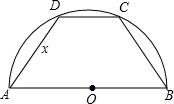如图，半径为1的半圆内接等腰梯形，其下底是半圆的直径，试求：
如图，半径为1的半圆O上有两个动点A，B，若AB=1，则四边形ABCD的面积的最大值是