题目内容
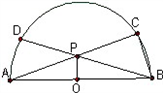
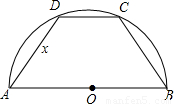
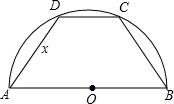 如图,半径为1的半圆内接等腰梯形,其下底是半圆的直径,试求:
如图,半径为1的半圆内接等腰梯形,其下底是半圆的直径,试求:(1)它的周长y与腰长x之间的函数关系式,并求出自变量x的取值范围.
(2)当腰长为何值时,周长有最大值?这个最大值为多少?
分析:(1)作OE⊥AD,DF⊥AO,垂足分别为E、F,由垂径定理可知AE=
AD=
x,由三角形相似得相似比,用x表示AF的长,根据CD=AB-2AF表示等腰梯形的上底,可求梯形的周长;
(2)把(1)中梯形周长的表达式配方,可求周长的最大值.
| 1 |
| 2 |
| 1 |
| 2 |
(2)把(1)中梯形周长的表达式配方,可求周长的最大值.
解答: 解:(1)作OE⊥AD,DF⊥AO,垂足分别为E、F,
解:(1)作OE⊥AD,DF⊥AO,垂足分别为E、F,
由垂径定理可知AE=
AD=
x,
易证Rt△ADF∽Rt△AOE,
∴
=
,即
=
,解得AF=
x2,
∴CD=AB-2AF=2-x2,
∴y=2x+2+2-x2=-x2+2x+4,
∵OA=1,AF=
x2,
∴
x2<1
∴0<x<
;
(2)∵y=-x2+2x+4=-(x-1)2+5,
∴x=1时,周长最大为5.
 解:(1)作OE⊥AD,DF⊥AO,垂足分别为E、F,
解:(1)作OE⊥AD,DF⊥AO,垂足分别为E、F,由垂径定理可知AE=
| 1 |
| 2 |
| 1 |
| 2 |
易证Rt△ADF∽Rt△AOE,
∴
| AF |
| AE |
| AD |
| AO |
| AF | ||
|
| x |
| 1 |
| 1 |
| 2 |
∴CD=AB-2AF=2-x2,
∴y=2x+2+2-x2=-x2+2x+4,
∵OA=1,AF=
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴0<x<
| 2 |
(2)∵y=-x2+2x+4=-(x-1)2+5,
∴x=1时,周长最大为5.
点评:本题考查了二次函数在求梯形周长最值中的运用.关键是利用垂径定理,三角形相似求梯形的上底.

练习册系列答案
相关题目
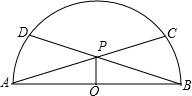 如图,半径为2的半圆O中有两条相等的弦AC与BD相交于点P.
如图,半径为2的半圆O中有两条相等的弦AC与BD相交于点P. 如图,半径为1的半圆O上有两个动点A,B,若AB=1,则四边形ABCD的面积的最大值是
如图,半径为1的半圆O上有两个动点A,B,若AB=1,则四边形ABCD的面积的最大值是