题目内容
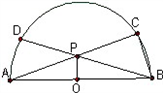
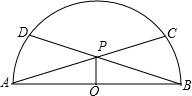 如图,半径为2的半圆O中有两条相等的弦AC与BD相交于点P.
如图,半径为2的半圆O中有两条相等的弦AC与BD相交于点P.(1)求证:PO⊥AB;
(2)若BC=1,求PO的长.
分析:(1)连接AD.因为AB是直径,所以△ABC、△ABD为直角三角形.根据“HL”判断它们全等,得∠BAC=∠ABD,从而PA=PB.根据等腰三角形性质得证;
(2)易证△AOP∽△ACB,运用相似三角形对应边成比例求解.
(2)易证△AOP∽△ACB,运用相似三角形对应边成比例求解.
解答: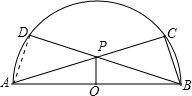 (1)证明:连接AD.
(1)证明:连接AD.
∵AB是直径,∴∠ACB=∠ADB=90°.
∵AC=BD,AB=BA,
∴△ABC≌△ABD.
∴∠BAC=∠ABD,从而PA=PB.
∵O是AB中点,
∴PO⊥AB;(4分)
(2)解:∵∠AOP=∠ACB=90°,∠OAP=∠CAB,
∴△AOP∽△ACB. (2分)
∴
=
.
∵AB=4,BC=1,∴AC=
=
.
∴OP=
=
. (2分)
 (1)证明:连接AD.
(1)证明:连接AD.∵AB是直径,∴∠ACB=∠ADB=90°.
∵AC=BD,AB=BA,
∴△ABC≌△ABD.
∴∠BAC=∠ABD,从而PA=PB.
∵O是AB中点,
∴PO⊥AB;(4分)
(2)解:∵∠AOP=∠ACB=90°,∠OAP=∠CAB,
∴△AOP∽△ACB. (2分)
∴
| OP |
| BC |
| AO |
| AC |
∵AB=4,BC=1,∴AC=
| 42-12 |
| 15 |
∴OP=
| 2 | ||
|
2
| ||
| 15 |
点评:此题考查了全等三角形的判定、等腰三角形的性质、相似三角形的判定和性质等知识点,综合性较强,难度偏上.

练习册系列答案
相关题目
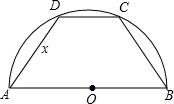 如图,半径为1的半圆内接等腰梯形,其下底是半圆的直径,试求:
如图,半径为1的半圆内接等腰梯形,其下底是半圆的直径,试求: 如图,半径为1的半圆O上有两个动点A,B,若AB=1,则四边形ABCD的面积的最大值是
如图,半径为1的半圆O上有两个动点A,B,若AB=1,则四边形ABCD的面积的最大值是