题目内容
13.已知抛物线y=ax2+bx+3与x轴的一个交点为A(-2,0),与x轴的另一个交点为B,与y轴交于点C,则能使△ABC为等腰三角形的抛物线的条数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据AB=AC,BA=BC,CA=CB分别画出图形,找出点B的位置,从而可确定出抛物线的条数.
解答 解:如图所示:
当AB=AC时,点B位于点B1或B3处;
当CA=CB时,点B位于点B4处;
当BA=BC时,点B位于点B2处.
∴点B的位置共有4处.
∴过三点的抛物线共有4条.
故选:C.
点评 本题主要考查的是等腰三角形的性质、抛物线与x轴的交点,分类讨论是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.某机械厂七月份的营业额为100万元,已知第三季度的总营业额共331万元.如果平均每月增长率为x,则由题意列方程应为( )
| A. | 100(1+x)2=331 | B. | 100+100×2x=331 | ||
| C. | 100+100×3x=331 | D. | 100[1+(1+x)+(1+x)2]=331 |
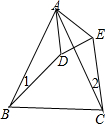 已知∠BAC=∠DAE,∠1=∠2,BD=CE.问△ABD≌△ACE吗?为什么?
已知∠BAC=∠DAE,∠1=∠2,BD=CE.问△ABD≌△ACE吗?为什么? 如图,101个正方形由小到大套在一起,从外向里相间地画上阴影,最外层画上阴影,最里面的一层画上阴影,最外面的正方形的边长为101cm,向里依次为100cm、99cm、…、1cm,那么在这个图形中,所有阴影部分的面积之和为多少?
如图,101个正方形由小到大套在一起,从外向里相间地画上阴影,最外层画上阴影,最里面的一层画上阴影,最外面的正方形的边长为101cm,向里依次为100cm、99cm、…、1cm,那么在这个图形中,所有阴影部分的面积之和为多少?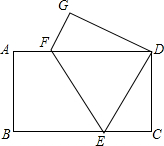 如图,长方形纸片ABCD,将纸片折叠使点A落在点G处,点B落在点D处,折痕为EF,若∠GFD:∠DFE=4:3,则∠DEC的度数为72°.
如图,长方形纸片ABCD,将纸片折叠使点A落在点G处,点B落在点D处,折痕为EF,若∠GFD:∠DFE=4:3,则∠DEC的度数为72°.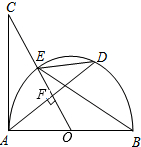 如图,AB为圆O的直径,过点O作弦AD的垂线交半圆O于点E,F为垂足,延长OE交AC于点C,使∠C=∠BED.
如图,AB为圆O的直径,过点O作弦AD的垂线交半圆O于点E,F为垂足,延长OE交AC于点C,使∠C=∠BED. 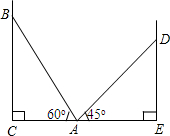 在两面墙之间有一个低端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点,已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE=$\sqrt{18}$m.
在两面墙之间有一个低端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点,已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE=$\sqrt{18}$m.