题目内容
当a≠0,b≠0且a≠b时,一次函数y=ax+b,y=bx+a和y=a的图象围成的图形的面积为______.
由题意,得
①
、②
或③
解①得
;
解②得
;
解③,得
,
∴A(1,a+b),B(
,a),C(0,a).
在△ABC中由三个顶点的坐标,得
BC=|
-0|=|
|,BC边上的高为:|a+b-a|=|b|,
∴S△ABC=
=|
|.
故答案为:|
|.
①
|
|
|
解①得
|
解②得
|
解③,得
|
∴A(1,a+b),B(
| a-b |
| a |
在△ABC中由三个顶点的坐标,得
BC=|
| a-b |
| a |
| a-b |
| a |
∴S△ABC=
|
| ||
| 2 |
| b(a-b) |
| 2a |
故答案为:|
| b(a-b) |
| 2a |

练习册系列答案
相关题目
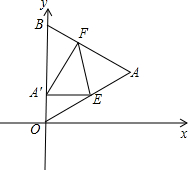 若能,请求出此时点A′的坐标;若不能,请你说明理由.
若能,请求出此时点A′的坐标;若不能,请你说明理由. 点M沿OA向终点A运动,点N沿BC向终点C运动,过点N作NP⊥BC,交AC于点P,连接MP,当两动点运动了t秒时.
点M沿OA向终点A运动,点N沿BC向终点C运动,过点N作NP⊥BC,交AC于点P,连接MP,当两动点运动了t秒时.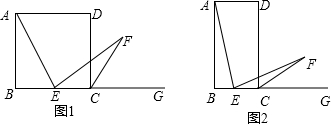
 如图,已知⊙O1与⊙O2相交于A、B两点,过A作⊙O1的切线交⊙O2于E,连接EB并延长交⊙O1于C,直线CA交⊙O2于点D.
如图,已知⊙O1与⊙O2相交于A、B两点,过A作⊙O1的切线交⊙O2于E,连接EB并延长交⊙O1于C,直线CA交⊙O2于点D.